Dispersion relation
A relation connecting certain magnitudes which characterize the scattering of particles with magnitudes characterizing their absorption. More exactly, the dispersion relation is a relation connecting the real part of the scattering amplitude (in the more general case, the Green function) with certain types of integrals of its imaginary part. Let a function 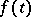 be absolutely integrable on the axis, and let it satisfy the causal relation
be absolutely integrable on the axis, and let it satisfy the causal relation 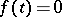 ,
, 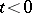 . Then its Fourier–Laplace transform
. Then its Fourier–Laplace transform
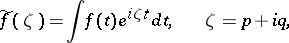 |
will be a holomorphic function in the upper half-plane 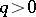 , and the real and imaginary parts of the boundary value
, and the real and imaginary parts of the boundary value 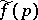 will satisfy the dispersion relation
will satisfy the dispersion relation
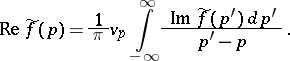 | (*) |
In describing real physical processes the dispersion relation of the type (*) becomes more complicated, since the function 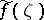 may increase at infinity as a polynomial (in this case a dispersion relation with subtractions is obtained), the boundary value
may increase at infinity as a polynomial (in this case a dispersion relation with subtractions is obtained), the boundary value 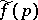 may be a generalized function of slow growth, while the number of variables may be more than one (multi-dimensional dispersion relations).
may be a generalized function of slow growth, while the number of variables may be more than one (multi-dimensional dispersion relations).
References
| [1] | N.N. Bogolyubov, B.V. Medvedev, M.K. Polivanov, "Questions in the theory of dispersion relations" , Moscow (1958) (In Russian) |
| [2] | V.S. Vladimirov, "Generalized functions in mathematical physics" , MIR (1979) (Translated from Russian) |
| [3] | N.N. Bogolyubov, A.A. Logunov, A.I. Oksak, I.T. Todorov, "General principles of quantum field theory" , Kluwer (1990) (Translated from Russian) |
Comments
A dispersion relation of the type defined here is often called a Kramers–Kronig relation. In the classical dispersion of light the relation gives a connection between the real (dispersive) and imaginary (absorptive) parts of the index of refraction.
Consider a linear wave equation such as the beam equation 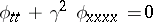 . For a sinusoidal wave train
. For a sinusoidal wave train 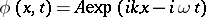 to satisfy such an equation some relation
to satisfy such an equation some relation 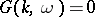 between the frequency and the wave number must hold. In this case
between the frequency and the wave number must hold. In this case 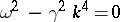 . This relation is called the dispersion relation. There are generalizations to non-linear wave equations, e.g., the KdV-equation, where the dispersion relation also involves the amplitude. Dispersion relations for waves are extensively discussed in [a5].
. This relation is called the dispersion relation. There are generalizations to non-linear wave equations, e.g., the KdV-equation, where the dispersion relation also involves the amplitude. Dispersion relations for waves are extensively discussed in [a5].
References
| [a1] | R. Kronig, J Opt. Soc. Amer , 12 (1926) pp. 547 |
| [a2] | H.A. Kramers, , Atti. Congr. Intern. Fisici Como , 2 (1927) pp. 545 |
| [a3] | N.G. van Kampen, "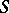 -matrix and causality condition I. Maxwell field" Phys. Rev. , 89 (1953) pp. 1072–1079 -matrix and causality condition I. Maxwell field" Phys. Rev. , 89 (1953) pp. 1072–1079 |
| [a4] | N.G. van Kampen, "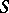 -matrix and causality condition II. Nonrelativistic particles" Phys. Rev. , 91 (1953) pp. 1267–1276 -matrix and causality condition II. Nonrelativistic particles" Phys. Rev. , 91 (1953) pp. 1267–1276 |
| [a5] | H. Bremermann, "Distributions, complex variables, and Fourier transforms" , Addison-Wesley (1965) |
| [a6] | G.B. Whitham, "Linear and non-linear waves" , Wiley (1974) |
Dispersion relation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dispersion_relation&oldid=46748