Disjunctive representations
disjoint representations
Unitary representations 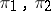 of a certain group or, correspondingly, symmetric representations of a certain algebra with an involution which satisfy the following equivalent conditions: 1) the unique bounded linear operator from the representation space of
of a certain group or, correspondingly, symmetric representations of a certain algebra with an involution which satisfy the following equivalent conditions: 1) the unique bounded linear operator from the representation space of 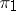 into the representation space of
into the representation space of 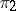 is equal to zero; or 2) no non-zero subrepresentations of the representations
is equal to zero; or 2) no non-zero subrepresentations of the representations  and
and 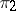 are equivalent. The concept of disjoint representations is fruitful in the study of factor representations; in particular, a representation
are equivalent. The concept of disjoint representations is fruitful in the study of factor representations; in particular, a representation  is a factor representation if and only if
is a factor representation if and only if 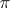 cannot be represented as the direct sum of two non-zero disjoint representations. Any two factor representations are either disjoint or else one of them is equivalent to a subrepresentation of the other (and, in the latter case, the representations are quasi-equivalent). The concept of disjoint representations plays an important role in the decomposition of a representation into a direct integral: If
cannot be represented as the direct sum of two non-zero disjoint representations. Any two factor representations are either disjoint or else one of them is equivalent to a subrepresentation of the other (and, in the latter case, the representations are quasi-equivalent). The concept of disjoint representations plays an important role in the decomposition of a representation into a direct integral: If 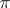 is a representation in a separable Hilbert space
is a representation in a separable Hilbert space 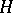 ,
, 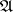 is the von Neumann algebra on
is the von Neumann algebra on 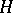 generated by the operators of the representation, and
generated by the operators of the representation, and 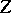 is the centre of
is the centre of 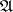 , then
, then
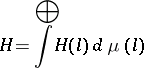 |
is the decomposition of the space  into the direct integral of Hilbert spaces, which corresponds to the decomposition
into the direct integral of Hilbert spaces, which corresponds to the decomposition
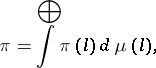 |
and if also the algebra 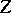 corresponds to the algebra of diagonalizable operators, then
corresponds to the algebra of diagonalizable operators, then 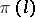 is a factor representation for almost-all
is a factor representation for almost-all 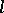 , and the representations
, and the representations 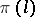 are pairwise disjoint for almost-all
are pairwise disjoint for almost-all 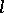 . There is a simple connection between the disjointness of two representations of a separable locally compact group (or of a separable algebra with an involution) and the mutual singularity of the representatives of canonical classes of measures on the quasi-spectrum of the group (algebra) corresponding to these representations.
. There is a simple connection between the disjointness of two representations of a separable locally compact group (or of a separable algebra with an involution) and the mutual singularity of the representatives of canonical classes of measures on the quasi-spectrum of the group (algebra) corresponding to these representations.
References
| [1] | J. Dixmier, "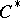 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
Comments
References
| [a1] | W. Arveson, "An invitation to 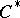 -algebras" , Springer (1976) -algebras" , Springer (1976) |
Disjunctive representations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Disjunctive_representations&oldid=46743