Disjunctive elements

independent elements

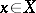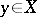Two elements and of a vector lattice with the property

Here

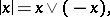which is equivalent to

The symbols 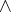and are, respectively, the disjunction and the conjunction. Two sets and are called disjunctive if any pair of elements , is disjunctive. An element 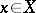is said to be disjunctive with a set 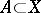if the sets 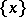and are disjunctive. A disjunctive pair of elements is denoted by or 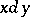; a disjunctive pair of sets is denoted by 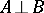or , respectively.

Example of disjunctive elements: The positive part 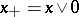and the negative part 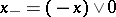of an element .

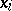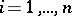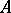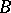If the elements , , are pairwise disjunctive, they are linearly independent; if and are disjunctive elements, the linear subspaces which they generate are also disjunctive; if , , and

exists, then . For disjunctive elements, several structural relations are simplified; e.g., if , then

for , etc.

The concept of disjunctive elements may also be introduced in more general partially ordered sets, such as Boolean algebras.

References

[1]	L.V. Kantorovich, B.Z. Vulikh, A.G. Pinsker, "Functional analysis in semi-ordered spaces" , Moscow-Leningrad (1950) (In Russian)
[2]	B.Z. Vulikh, "Introduction to the theory of partially ordered spaces" , Wolters-Noordhoff (1967) (Translated from Russian)
[3]	N. Bourbaki, "Elements of mathematics. Integration" , Addison-Wesley (1975) pp. Chapt.6;7;8 (Translated from French)

Comments

The phrase "disjunctive sets" also has a different meaning, cf. Disjunctive family of sets.

References

[a1]	W.A.J. Luxemburg, A.C. Zaanen, "Riesz spaces" , I , North-Holland (1971)