Discriminant function

A statistic for the construction of a rule for distinguishing in problems of discriminant analysis involving two distributions. The discrimination problem for two distributions may be stated as follows. Let an observed object with vector of measurements 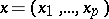belong to one of the sets 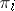, , 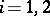and let it be unknown to which one. The problem is to find a rule which would make it possible to assign the object to 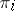if the observed value of the vector is known (the discrimination rule). The construction of such a rule is based on subdivision of the sampling space for the vector into domains 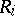, , 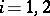such that, if is found in 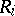, it is reasonable (from the point of view of the chosen principle for an optimal solution) to assign to 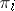. If the discrimination rule is based on the subdivision , , 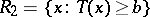where and 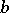are constants and 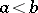, the statistic 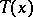is called the discriminant function, while the domain in which 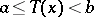is called the uncertainty zone. Linear discriminant functions, which are simple to handle, are particularly important. If the distributions are normal and have equal covariance matrices, the discriminant function will be linear if the optimality requirements of the discrimination rule are reasonable. The concept of a discriminant informant is introduced in the problem of discriminant analysis with multiple distributions when the Bayesian approach is adopted.