Directing functionals, method of

A special method for proving theorems about eigen function expansions of self-adjoint differential operators. In the special case of a second-order singular differential operator on the positive semi-axis, the corresponding theorem was first obtained by H. Weyl [1]. The general theorem for a differential operator of order 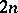was first proved by M.G. Krein [2], who used the method now known as the method of directing functionals. The result may be formulated as follows (see [3]). 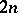Let be a self-adjoint differential expression of order on an interval 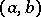, let 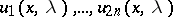be the system of solutions of the equation

satisfying the initial conditions

where 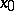is a fixed point in 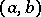and 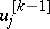is the -th quasi-derivative of . Then, for any self-adjoint extension 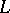of the operator generated by , there exists a matrix-valued distribution function

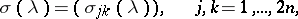such that, for any function ,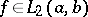

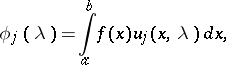(1)

(2)

where the integrals in (1) and (2) are assumed to be convergent in the sense of the metrics in 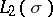and , respectively. Under these assumptions, one has the following analogue of Parseval's equality:

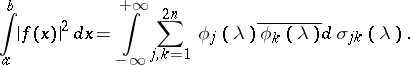The functionals , defined on functions in with compact support, are called the directing functionals of .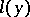

The generalization and further development of the method of directing functionals gave rise to the concept of rigged Hilbert spaces and generalized eigen element expansions (see [4], [5], [6]).

References

[1]	H. Weyl, "Ueber gewöhnliche Differentialgleichungen mit Singularitäten und die zugehörigen Entwicklungen willkürlicher Funktionen" Math. Ann. , 68 (1910) pp. 220–269
[2]	M.G. Krein, "On a general method for decomposing Hermitian positive kernels into elementary factors" Dokl. Akad. Nauk SSSR , 53 : 1 (1946) pp. 3–6 (In Russian)
[3]	M.A. Naimark, "Lineare Differentialoperatoren" , Akademie Verlag (1960) (Translated from Russian)
[4]	Yu.M. [Yu.M. Berezanskii] Berezanskiy, "Expansion in eigenfunctions of selfadjoint operators" , Amer. Math. Soc. (1968) (Translated from Russian)
[5]	I.M. Gel'fand, G.E. Shilov, "Some problems in differential equations" , Moscow (1958) (In Russian)
[6]	I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , 4 , Acad. Press (1964) (Translated from Russian)
[7]	B.M. Levitan, "Eigenfunction expansions of second-order differential equations" , Moscow-Leningrad (1950) (In Russian)