Dimension invariant

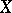An integer , defined for every topological space of a given class 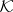, which has sufficiently many properties to make it resemble the usual notion of dimension: the number of coordinates of higher-dimensional Euclidean spaces. Here one requires of the class 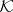that it contains all cubes with any number of coordinates, and together with any space 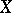which is an element of it, it should also contain as an element every space homeomorphic to 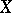. For a dimension invariant 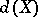it is assumed, in any case, that for homeomorphic spaces 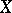and 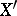one always has 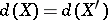, and that for the -dimensional cube 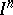one has 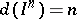. Among the dimension invariants, the most important ones are the so-called classical dimensions — the Lebesgue dimension 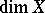and the (large and small) inductive dimensions (cf. Inductive dimension) , .

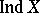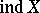The following propositions distinguish 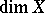from all other dimension invariants defined, respectively, in the class of all (metric) compacta, all metrizable and all separable metrizable spaces, and hence settle for these spaces the problem of the axiomatic definition of dimension. The only dimension invariant 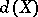satisfying the conditions 1), 2), 3) listed below and defined in the class 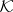of all (metric) compacta 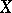is the dimension 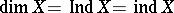(Aleksandrov's theorem).

Condition 1) (Poincaré's axiom). If a space 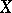is of class 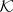and if 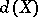is equal to the non-negative integer , then 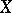contains a closed subspace 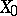for which 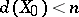and such that the set 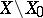is disconnected.

Condition 2) (the finite sum axiom). If a space 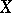of class 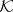is the union of two closed subspaces 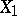and 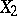for which 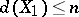, , 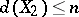then also .

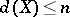Condition 3) (Brouwer's axiom in metric form). If 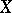is a space belonging to 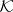and if 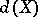is the non-negative integer , then there is a positive number such that for every space 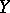which is the image of 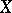under some -mapping one has the inequality 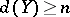. Here a mapping 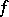from a compactum 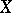onto a compactum 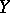is called an -mapping if it is continuous and if the complete pre-image 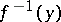of every point 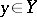has diameter 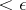in .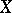

Shchepin's theorem [2]. The dimension 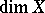is the only dimension invariant 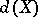defined, respectively, in the class 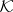of all metric, or all separable metric spaces 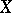, which satisfies the following conditions (Shchepin's theorem):

Condition 1) (Poincaré's axiom). See above.

Condition 2) (the countable sum axiom). If a space 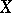belonging to the class 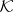is the union of a countable number of closed subspaces , 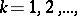each having , then also .

Condition 3) (Brouwer's axiom in general form). If for a space 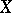belonging to the class 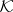one has 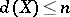, then there is a finite open covering of 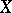such that for every space 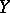belonging to 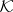and which is the image of 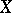under some 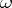-mapping one has 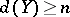. Here a mapping 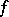from a space 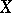on which a certain open covering 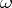has been fixed onto a space 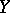is called an 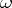-mapping if every point 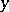of 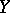has a neighbourhood 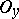whose complete pre-image is contained in some element of .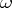

References

[1]	P.S. Aleksandrov, "Some old problems in homological dimension theory" , Proc. Internat. Symp. Topology and its Applications. Herzog-Novi, 1968 , Beograd (1969) pp. 38–42 (In Russian)
[2]	E. [E. Shchepin] Ščepin, "Axiomatics of the dimension of metric spaces" Soviet Math. Dokl. , 13 (1972) pp. 1177–1179 Dokl. Akad. Nauk SSSR , 206 : 1 (1972) pp. 31–32
[3]	P.S. Aleksandrov, B.A. Pasynkov, "Introduction to dimension theory" , Moscow (1973) (In Russian)

Comments

A brief discussion of axioms for dimension invariants can also be found in [a1].

References

[a1]	R. Engelking, "Dimension theory" , North-Holland & PWN (1978)