Dimension, additive properties of
Properties expressing a connection between the dimension of a topological space  that can be represented as the sum of subspaces
that can be represented as the sum of subspaces 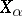 with the dimensions of these subspaces
with the dimensions of these subspaces 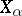 . There are several types of additive properties of dimension.
. There are several types of additive properties of dimension.
The countable closed sum theorem. If a normal Hausdorff space  can be represented as a finite or countable sum of closed subsets
can be represented as a finite or countable sum of closed subsets 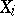 , then
, then
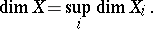 |
If 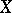 is also perfectly normal or hereditarily paracompact, then
is also perfectly normal or hereditarily paracompact, then
 |
The locally finite closed sum theorem. If a normal Hausdorff space  can be represented as the sum of a locally finite system of closed subsets
can be represented as the sum of a locally finite system of closed subsets 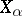 , then
, then
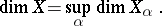 |
If  is also perfectly normal and hereditarily paracompact, then
is also perfectly normal and hereditarily paracompact, then
 |
The addition theorem. If the space 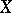 is Hausdorff, hereditarily normal and if
is Hausdorff, hereditarily normal and if 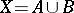 , then
, then
 |
(the Menger–Urysohn formula). If  is also perfectly normal, then
is also perfectly normal, then
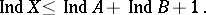 |
A metric space 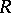 has dimension
has dimension 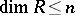 if and only if
if and only if
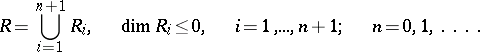 |
If  is hereditarily normal and Hausdorff, then for any closed subset
is hereditarily normal and Hausdorff, then for any closed subset 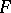 one has
one has
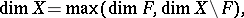 |
 |
Comments
See also Dimension; Dimension theory.
References
| [a1] | R. Engelking, "Dimension theory" , North-Holland & PWN (1978) |
Dimension, additive properties of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dimension,_additive_properties_of&oldid=46704