Differentiation along the flow of a dynamical system
An operator defined as follows. Let
 | (*) |
be an autonomous system, let  , let
, let 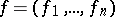 , and let
, and let 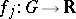 be smooth mappings, where
be smooth mappings, where  is a domain in
is a domain in 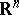 . Let a smooth mapping
. Let a smooth mapping 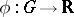 be given. The derivative
be given. The derivative 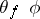 along the flow of the system (*) of
along the flow of the system (*) of 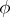 at a point
at a point 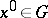 is defined by
is defined by
 |
where 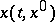 is a solution of the system (*) such that
is a solution of the system (*) such that 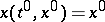 . The operator
. The operator 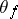 displays the following properties: 1) linearity in
displays the following properties: 1) linearity in  ; and 2)
; and 2) 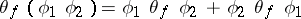 . The function
. The function 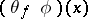 coincides with the derivative of
coincides with the derivative of  with respect to the vector field
with respect to the vector field  .
.
References
| [1] | L.S. Pontryagin, "Ordinary differential equations" , Addison-Wesley (1962) (Translated from Russian) |
Comments
In terms of the canonical basis 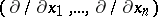 of the tangent space
of the tangent space 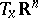 at a point
at a point  , the vector field
, the vector field  is written
is written
 |
This first-order differential operator defines a derivation of the ring (cf. Derivation in a ring) of smooth functions  into itself. Moreover, this sets up a bijective correspondence between vector fields on
into itself. Moreover, this sets up a bijective correspondence between vector fields on 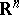 and derivations on
and derivations on  . Using local coordinates this extends to the case of smooth differentiable manifolds. And indeed it is quite customary to define vector fields on a manifold
. Using local coordinates this extends to the case of smooth differentiable manifolds. And indeed it is quite customary to define vector fields on a manifold  as derivations of
as derivations of  and to observe subsequently that the notion corresponds to a section of the tangent bundle. In this setting a tangent vector at
and to observe subsequently that the notion corresponds to a section of the tangent bundle. In this setting a tangent vector at 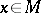 can be defined as a derivation on the local algebra of germs of smooth functions at
can be defined as a derivation on the local algebra of germs of smooth functions at  on
on  . Thus, differentiation along the flow of a dynamical system given by the vector field
. Thus, differentiation along the flow of a dynamical system given by the vector field  simply means applying the derivation on
simply means applying the derivation on 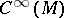 given by
given by  .
.
References
| [a1] | Y. Choquet-Bruhat, C. DeWitt-Morette, M. Dillard-Bleick, "Analysis, manifolds and physics" , North-Holland (1977) pp. Sect. III.B (Translated from French) |
Differentiation along the flow of a dynamical system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differentiation_along_the_flow_of_a_dynamical_system&oldid=46697