Differential equation with total differential
An ordinary differential equation
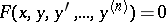 | (1) |
whose left-hand side is a total derivative:
 |
In other words, equation (1) is a differential equation with total differential if there exists a differentiable function 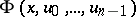 such that
such that
 |
identically with respect to all arguments. The solution of a differential equation with total differential of order  is reduced to solving an equation of order
is reduced to solving an equation of order 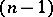 :
:
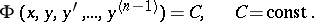 |
Let  be an
be an  times continuously-differentiable function and let
times continuously-differentiable function and let 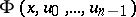 be a function having continuous partial derivatives up to and including the second order. Let
be a function having continuous partial derivatives up to and including the second order. Let
 |
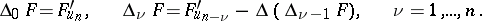 |
For equation (1) to be a differential equation with total differential it is sufficient that the functions  ,
, 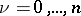 , are independent of
, are independent of  and that
and that 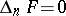 [1]. In particular,
[1]. In particular, 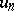 may enter
may enter 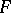 in a linear manner only.
in a linear manner only.
The first-order equation
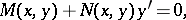 | (2) |
where the functions 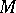 ,
, 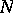 ,
,  , and
, and 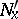 are defined and continuous in an open simply-connected domain
are defined and continuous in an open simply-connected domain 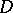 of the
of the 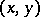 -plane and
-plane and  in
in 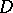 , is a differential equation with total differential if and only if
, is a differential equation with total differential if and only if
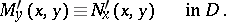 |
The general solution of equation (2) with total differential has the form  , where
, where
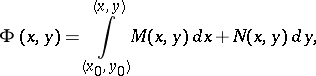 |
and the integral is taken over any rectifiable curve lying inside 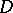 and joining an arbitrary fixed point
and joining an arbitrary fixed point  with the point
with the point 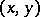 [2]. Equation (2) (in the general case, an equation (1) which is linear with respect to
[2]. Equation (2) (in the general case, an equation (1) which is linear with respect to 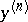 ) can, under certain conditions, be reduced to a differential equation with total differential by multiplying by an integrating factor.
) can, under certain conditions, be reduced to a differential equation with total differential by multiplying by an integrating factor.
References
| [1] | E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1947) |
| [2] | N.P. Erugin, "A general course in differential equations" , Minsk (1972) (In Russian) |
Differential equation with total differential. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_equation_with_total_differential&oldid=46680