Differential calculus (on analytic spaces)

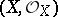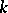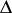A generalization of the classical calculus of differential forms and differential operators to analytic spaces. For the calculus of differential forms on complex manifolds see Differential form. Let be an analytic space over a field , let be the diagonal in 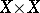, let 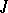be the sheaf of ideals defining 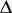and generated by all germs of the form 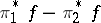, where 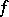is an arbitrary germ from 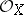, and let 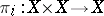be projection on the -th factor.

The analytic sheaf 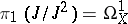is known as the sheaf of analytic differential forms of the first order on 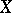. If 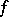is the germ of an analytic function on 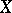, then the germ 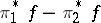belongs to 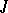and defines the element 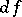of 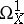known as the differential of the germ 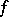. This defines a sheaf homomorphism of vector spaces 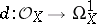. If 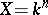, then 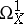is the free sheaf generated by 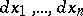, where are the coordinates in 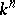. If 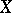is an analytic subspace in 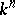, defined by a sheaf of ideals 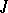, then

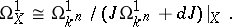Each analytic mapping 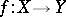may be related to a sheaf of relative differentials 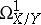. This is the analytic sheaf 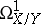inducing 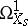on each fibre 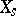(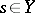) of 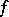; it is defined from the exact sequence

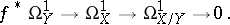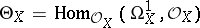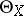The sheaf is called the sheaf of germs of analytic vector fields on . If is a manifold, and are locally free sheaves, which are naturally isomorphic to the sheaf of analytic sections of the cotangent and the tangent bundle over 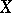, respectively.

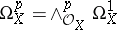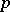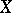The analytic sheaves are called sheaves of analytic exterior differential forms of degree on (if 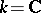, they are also called holomorphic forms). For any 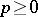one may define a sheaf homomorphism of vector spaces 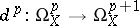, which for 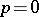coincides with the one introduced above, and which satisfies the condition 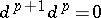. The complex of sheaves 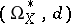is called the de Rham complex of the space 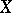. If 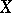is a manifold and 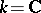or 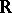, the de Rham complex is an exact complex of sheaves. If 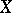is a Stein manifold or a real-analytic manifold, the cohomology groups of the complex of sections 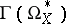, which is also often referred to as the de Rham complex, are isomorphic to .

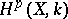If 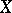has singular points, the de Rham complex need not be exact. If 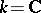, a sufficient condition for the exactness of the de Rham complex at a point 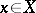is the presence of a complex-analytic contractible neighbourhood at . The hyperhomology groups of the complex 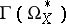contain, for 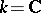, the cohomology groups of the space 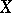with coefficients in 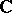as direct summands, and are identical with them if 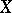is smooth. The sections of the sheaf 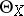are called analytic (and if 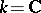, also holomorphic) vector fields on 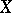. For any open 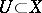the field 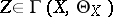defines a derivation in the algebra of analytic functions 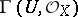, acting according to the formula 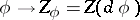. 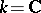If or 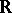, then 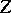defines a local one-parameter group 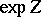of automorphisms of the space 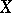. If, in addition, 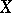is compact, the group 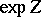is globally definable.

The space 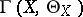provided with the Lie bracket is a Lie algebra over 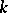. If 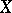is a compact complex space, 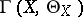is the Lie algebra of the group .

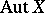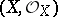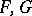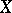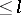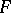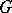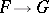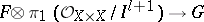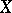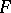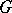Differential operators on an analytic space are defined in analogy to the differential operators on a module (cf. Differential operator on a module). If are analytic sheaves on , then a linear differential operator of order , acting from into , is a sheaf homomorphism of vector spaces which extends to an analytic homomorphism . If is smooth and and are locally free, this definition gives the usual concept of a differential operator on a vector bundle , [4].

The germs of the linear differential operators 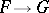form an analytic sheaf 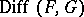with filtration

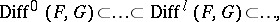where 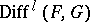is the sheaf of germs of operators of order 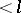. In particular, 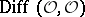is a filtered sheaf of associative algebras over 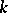under composition of mappings. One has

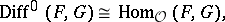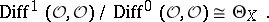The sheaf 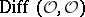was studied (for the non-smooth case) only for certain special types of singular points. In particular, it was proved in the case of an irreducible one-dimensional complex space 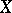that the sheaf of algebras 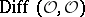and the corresponding sheaf of graded algebras have finite systems of generators [5].

References

[1]	B. Malgrange, "Analytic spaces" Enseign. Math. Ser. 2 , 14 : 1 (1968) pp. 1–28
[2]	W. Kaup, "Infinitesimal Transformationsgruppen komplexer Räume" Math. Ann. , 160 : 1 (1965) pp. 72–92
[3a]	L. Schwartz, "Variedades analiticas complejas elipticas" , Univ. Nac. Colombia (1956)
[3b]	L. Schwartz, "Ecuaciones differenciales parciales" , Univ. Nac. Colombia (1956)
[4]	R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980)
[5]	Th. Bloom, "Differential operators on curves" Rice Univ. Stud. , 59 : 2 (1973) pp. 13–19
[6]	R. Berger, R. Kiehl, E. Kunz, H.-J. Nastold, "Differentialrechnung in der analytischen Geometrie" , Springer (1967)
[7]	G. Fischer, "Complex analytic geometry" , Springer (1976)