Difference cochain and chain
A difference cochain is an obstruction to the extension of a homotopy between mappings. Let 
be some cellular space, let 
be a simply-connected topological space and suppose, moreover, that one is given two mappings 
and a homotopy
 |
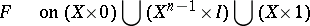(where 
and 
is the 
-dimensional skeleton of 
) between these mappings on the 
-dimensional skeleton. For every oriented 
-dimensional cell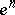 
of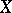 
, the restriction of 
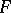to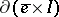 
gives a mapping 
(
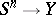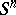is the 
-dimensional sphere) and hence an element of the group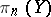 
. Thus there arises the cochain 
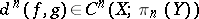(the notation 
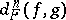would be more precise), which is called the difference cochain; the cochain 
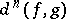is an obstruction to the extension of 
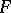to
 |
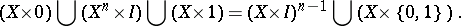The following statements hold: 1)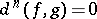 
if and only if the homotopy between 
and 
can be extended to 
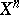; 2) the cochain
 |
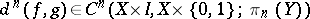is a cocycle; 3) the cohomology class
 |
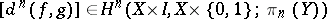vanishes if and only if there is a homotopy between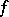 
and 
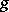on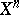 
that coincides with 
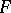on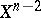 
. Without loss of generality one can assume that 
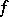and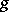 
coincide on 
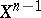and that 
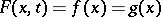for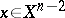 
. Then the following statements hold:
1) 
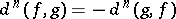, in particular 
;
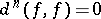2) 
;
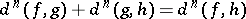3) for any mapping 
and for any cochain 
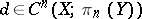there is a mapping 
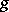for which 
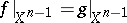and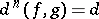 
.
Now suppose one is given two mappings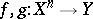 
, 
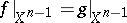and let 
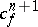and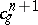 
be the obstructions to the extensions of the corresponding mappings. The role of the difference cochain in the theory of obstructions is explained by the following proposition:
 |
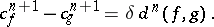Thus, if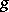 
can be extended to 
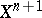, then 
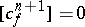and if 
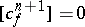, then 
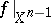can be extended to 
.
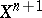Comments
References
| [a1] | G.W. Whitehead, "Elements of homotopy theory" , Springer (1978) pp. 228 |
Difference cochain and chain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Difference_cochain_and_chain&oldid=46652