Diagram

in a category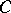

A mapping 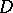of an oriented graph 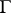with set of vertices 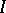and set of edges 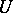into the category 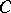for which

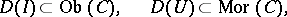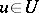and if the edge has source (origin) 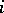and target (end) 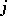. The concept of a diagram in 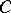may also be defined as the image of the mapping 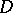, in order to obtain a better visualization of diagrams.

Let 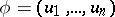be an oriented chain of the graph 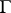with source and target 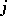, i.e. a non-empty finite sequence of edges in which the source of each edge coincides with the target of the preceding one; also, let 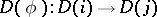denote the composition of morphisms

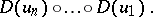The diagram 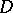is said to be commutative if 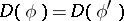for any two oriented chains 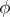and with identical source and target.

The most frequently encountered forms of diagrams are sequences, triangular diagrams and square diagrams. To define a sequence, the defining graph is taken to have the form

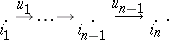The corresponding diagram is represented as follows:

where the 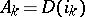are objects in the category 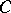, while the 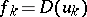are morphisms in this category.

A triangular diagram in a category 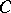corresponds to the graph

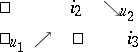and is represented as follows:

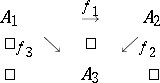Commutativity of this diagram means that .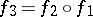

A square diagram corresponds to the graph

and is represented as follows:

Commutativity of this diagram means that .

The class of diagrams with a given graph forms a category. A morphism of a diagram into a diagram 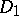is taken to be a family of morphisms 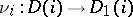, where 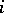runs through the set of vertices of 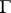, so that for any edge with source and target 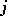the condition 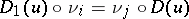is met. In particular, one may speak of isomorphic diagrams. The graph 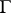is sometimes referred to as the scheme of a diagram in .

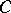References

[1]	A. Grothendieck, "Sur quelques points d'algèbre homologique" Tohoku Math. J. , 9 (1957) pp. 119–221

References

[a1]	H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956)
[a2]	S. MacLane, "Categories for the working mathematician" , Springer (1971) pp. Chapt. IV, Sect. 6; Chapt. VII, Sect. 7