Diagonal subgroup
From Encyclopedia of Mathematics
The subgroup of a Cartesian power of a given group  consisting of all elements with identical components. For instance, the diagonal group of the product
consisting of all elements with identical components. For instance, the diagonal group of the product 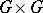 is the group of pairs
is the group of pairs 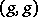 ,
, 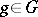 .
.
Comments
The phrase diagonal group (or diagonal subgroup) is also used for the subgroup scheme  of
of  over a field
over a field 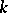 whose points with values in a
whose points with values in a  -algebra
-algebra  are the diagonal invertible matrices with coefficients in
are the diagonal invertible matrices with coefficients in 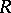 .
.
Let 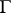 be a commutative group. The functor
be a commutative group. The functor 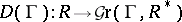 from commutative rings with unit element to groups then defines a group scheme. Here
from commutative rings with unit element to groups then defines a group scheme. Here  is the group of invertible elements of
is the group of invertible elements of 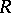 and
and 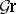 is the category of groups. Group schemes isomorphic to such group schemes are called diagonizable group schemes.
is the category of groups. Group schemes isomorphic to such group schemes are called diagonizable group schemes.
References
| [a1] | M. Demazure, P. Gabriel, "Groupes algébriques" , 1 , North-Holland (1970) |
How to Cite This Entry:
Diagonal subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Diagonal_subgroup&oldid=46643
Diagonal subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Diagonal_subgroup&oldid=46643
This article was adapted from an original article by Yu.I. Merzlyakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article