Determinant variety

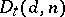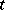The set of matrices of dimension and of a rank lower than , with the structure of an algebraic variety. Let be the ideal in the ring of polynomials

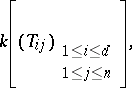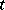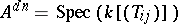with coefficients in a field , generated by the -order minors of the matrix of dimension constituted by the variables (a determinant ideal). The set of zeros of the ideal in the affine space is known as the determinant variety and is denoted by 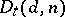. For any commutative -algebra 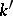the set of 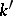-points of the determinant variety 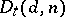coincides, in a natural manner, with the set of matrices of dimension and rank with coefficients in .

The following are special cases of determinant varieties: 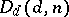is the hypersurface in defined by the vanishing of the determinant of a square matrix of dimension 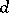consisting of independent variables (a determinant hypersurface); is an affine cone for the image of the Segre imbedding

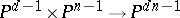of the product of projective spaces [2].

Determinant varieties have the following properties: 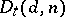is irreducible, reduced (i.e. the ideal is simple), is a Cohen–Macaulay variety (cf. Cohen–Macaulay ring), is normal, and the dimension of 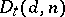is equal to [1], [2]. 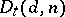is a Gorenstein scheme if and only if 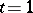or 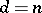(cf. Gorenstein ring) [5]. Determinant varieties are closely connected with Schubert varieties of a Grassmann manifold (cf. Schubert variety).

References

[1]	M. Hochster, J. Eagon, "Cohen–Macaulay rings, invariant theory, and the generic perfection of determinantal loci" Amer. J. Math. , 93 : 4 (1971) pp. 1020–1058
[2]	S. Kleiman, J. Landolfi, "Geometry and deformation of special Schubert varieties" Compositio Math. , 23 (1971) pp. 407–434
[3]	D. Laksov, "Deformation of determinantal schemes" Compositio Math. , 30 (1975) pp. 273–292
[4]	C. Musili, "Some properties of Schubert varieties" J. Indian Math. Soc. , 38 (1974) pp. 131–145
[5]	T. Svanes, "Coherent cohomology on Schubert subschemes of flag schemes and applications" Adv. in Math. , 14 (1974) pp. 369–453

Comments

Many geometrical properties of determinant varieties can be found in [a1]. Instead of determinant variety, etc. one also speaks of determinantal variety, etc.

References

[a1]	T.G. Room, "Geometry of determinantal loci" , Cambridge Univ. Press (1938)