Derived automorphism
in ergodic theory
A transformation 
defined by using an automorphism 
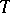of a measure space 
and a measurable subset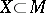 
of positive measure such that almost-all points of 
return to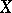 
under the action of iterates of 
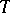. For every such point 
its image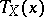 
is defined as that point of the trajectory 
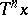at which this trajectory returns to 
for the first time after 
(according to the Poincaré recurrence theorem, cf. Poincaré return theorem, the condition for almost-all points of 
to return to 
at some time is automatically satisfied if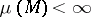 
). The transformation 
turns out to be an automorphism (more precisely, an automorphism modulo 
) of the space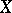 
with the measure induced on it (this measure is the measure 
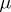considered only on subsets of 
; if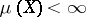 
then this measure is usually normalized).
Conversely, if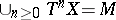 
(this condition is automatically satisfied if the automorphism 
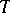is ergodic), then the original automorphism 
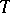can be recovered (up to conjugation by means of an isomorphism of measure spaces) from 
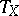and the time of first return
 |
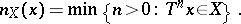Namely,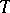 
is the special automorphism constructed from 
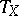and 
.
Comments
For automorphism of a measure space cf. Measure-preserving transformation.
In the literature also induced or derivative automorphism are used. See [a1] or [a2].
References
| [a1] | S. Kakutani, "Induced measure preserving transformations" Proc. Japan. Acad. , 19 (1943) pp. 635–641 |
| [a2] | K. Petersen, "Ergodic theory" , Cambridge Univ. Press (1983) pp. 39 |
Derived automorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Derived_automorphism&oldid=46633