Density matrix
of a state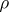 
defined on the algebra 
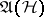of bounded linear operators acting on a Hilbert space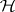 
The positive nuclear operator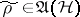 
such that
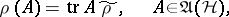 | (1) |
where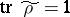 
. Conversely, any state 
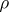, i.e. any linear positive 
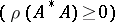normalized 
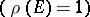functional on 
, can be represented in the form (1), i.e. it has a density matrix 
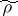, which is moreover unique.
The concept of a density matrix arose in statistical physics in defining a Gibbs quantum state. Let a quantum system occupying a finite volume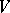 
in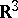 
be described by the vectors of a certain Hilbert space 
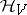, by the Hamiltonian 
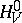and, possibly, by some set of mutually commuting "first integrals" 
, 
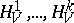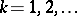. A Gibbs state for such a system is a state on 
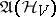defined by the density matrix
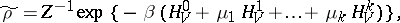 | (2) |
where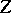 
is a normalizing factor and 
, 
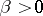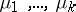are real parameters.
In addition to the density matrix (2), the state of a system in quantum statistical physics may be defined by means of the so-called reduced density matrix. In the simplest case of a system of identical particles (bosons or fermions) described by the vectors of a Fock [Fok] space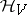 
, the reduced density matrix 
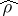of a state 
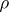is the set of (in general, generalized) functions
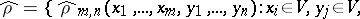 | (3) |
 |
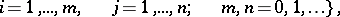where
 |
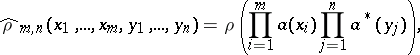and where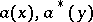 
, 
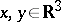, are the creation operators and annihilation operators, respectively, acting in 
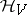. If the creation and annihilation operators in 
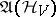are replaced by some other system of generators 
(
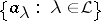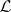is a certain set of indices), then the reduced density matrix 
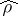for a state 
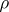is defined by analogy with (3) as the set of values of 
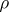on all possible monomials of the form
 |
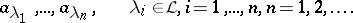The reduced density matrix is particularly convenient for determining the limiting Gibbs state in a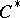 
-algebra 
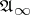of so-called quasi-local observables: 
(the bar denotes closure in the uniform topology).
References
| [1] | L.D. Landau, E.M. Lifshitz, "Statistical physics" , Pergamon (1980) (Translated from Russian) |
| [2] | D. Ruelle, "Statistical mechanics: rigorous results" , Benjamin (1974) |
Comments
The statement that any state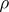 
has a representation (1) has been proved for finite-dimensional 
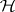only.
The functions defined by (3) are the quantum analogues of distribution functions.
Density matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Density_matrix&oldid=46627