The Dini derivatives (cf. Dini derivative) of any finite function 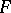 at almost any point
at almost any point  satisfy one of the following relations:
satisfy one of the following relations:
The theorem has been demonstrated by A. Denjoy for continuous functions [1]. The theorem, cf. [2], which follows is a generalization of Denjoy's theorem: For almost-all  the contingent of the graph of
the contingent of the graph of 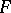 at a point
at a point  is one of the following figures: a plane, a half-plane (with a non-vertical boundary line) or a straight line (non-vertical).
is one of the following figures: a plane, a half-plane (with a non-vertical boundary line) or a straight line (non-vertical).
References
| [1] | A. Denjoy, "Mémoire sur les nombres dérivés des fonctions continues" J. Math. Pures Appl. (7) , 1 (1915) pp. 105–240 |
| [2] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) |
The theorem cited is often called the Denjoy–Young–Saks theorem. It was discovered and proved, for continuous 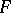 , independently of Denjoy by G.C. Young [a2]. She then extended it to measurable
, independently of Denjoy by G.C. Young [a2]. She then extended it to measurable 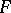 [a3]. S. Saks extended the theorem to arbitrary functions
[a3]. S. Saks extended the theorem to arbitrary functions 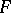 [a1].
[a1].
References
| [a1] | S. Saks, "Sur les nombres derivées des fonctions" Fund. Math. , 5 (1924) pp. 98–104 |
| [a2] | G.C. Young, Quart. J. Math , 47 (1916) pp. 148–153 |
| [a3] | G.C. Young, "On the derivatives of a function" Proc. London Math. Soc. (2) , 15 (1916) pp. 360–384 |
How to Cite This Entry:
Denjoy theorem on derivatives. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Denjoy_theorem_on_derivatives&oldid=46625
This article was adapted from an original article by T.P. Lukashenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article at almost any point
at almost any point  satisfy one of the following relations:
satisfy one of the following relations:

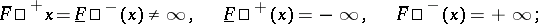

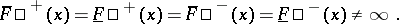
 the contingent of the graph of
the contingent of the graph of 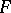 at a point
at a point  is one of the following figures: a plane, a half-plane (with a non-vertical boundary line) or a straight line (non-vertical).
is one of the following figures: a plane, a half-plane (with a non-vertical boundary line) or a straight line (non-vertical).
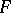 , independently of Denjoy by G.C. Young [a2]. She then extended it to measurable
, independently of Denjoy by G.C. Young [a2]. She then extended it to measurable 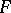 [a3]. S. Saks extended the theorem to arbitrary functions
[a3]. S. Saks extended the theorem to arbitrary functions 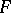 [a1].
[a1].