Delta amplitude
From Encyclopedia of Mathematics
One of the three fundamental Jacobi elliptic functions. It is denoted by
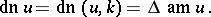 |
The delta amplitude is expressed as follows in terms of the Weierstrass sigma-function, the Jacobi theta-functions or a series:
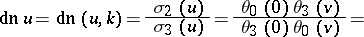 |
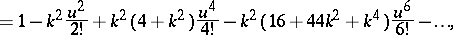 |
where 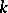 is the modulus of the delta amplitude,
is the modulus of the delta amplitude, 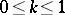 , and
, and 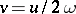 ,
, 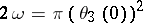 . If
. If 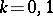 one has, respectively,
one has, respectively,
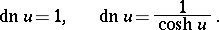 |
See also Weierstrass elliptic functions; Elliptic function.
References
| [1] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , Springer (1964) pp. Chapt. 3, Abschnitt 2 |
Comments
References
| [a1] | H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , Higher transcendental functions , 2. Bessel functions, parabolic cylinder functions, orthogonal polynomials , McGraw-Hill (1953) pp. Chapt. 13 |
How to Cite This Entry:
Delta amplitude. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Delta_amplitude&oldid=46622
Delta amplitude. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Delta_amplitude&oldid=46622
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article