Degeneration, probability of
From Encyclopedia of Mathematics
The probability of no particles being left in a branching process at an epoch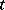 
. Let 
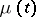be the number of particles in a branching process with one type of particles. The probability of degeneration
 |
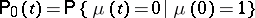does not decrease as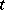 
increases; the value
 |
is called the probability of degeneration in infinite time or simply the probability of degeneration. If 
is the time elapsing from the beginning of the process to the epoch of disappearance of the last particle, then 
and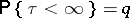 
. The rate of convergence of 
to 
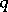as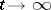 
has been studied for various models of branching processes.
Comments
The probability of degeneration is more commonly called the probability of extinction (in infinite time).
References
| [a1] | P.E. Ney, K.B. Athreya, "Branching processes" , Springer (1972) |
| [a2] | T.E. Harris, "The theory of branching processes" , Springer (1963) |
How to Cite This Entry:
Degeneration, probability of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Degeneration,_probability_of&oldid=46617
Degeneration, probability of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Degeneration,_probability_of&oldid=46617
This article was adapted from an original article by V.P. Chistyakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article