Degenerate kernels, method of

A method to construct an approximating equation for approximate (and numerical) solutions of certain kinds of linear and non-linear integral equations. The main type of integral equations suitable for solving by this method are linear one-dimensional integral Fredholm equations of the second kind. The method as applied to such equations consists of an approximation which replaces the kernel 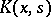of the integral equation

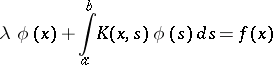(1)

by a degenerate kernel of the type

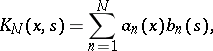followed by the solution of the Fredholm degenerate integral equation

(2)

Solving (2) is reduced to solving a system of linear algebraic equations. The degenerate kernel 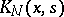may be found from the kernel 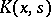in several ways, e.g. by expanding the kernel into a Taylor series or a Fourier series (for other methods see Bateman method; Strip method (integral equations)).

The method of degenerate kernels may be applied to systems of integral equations of the type (1), to multi-dimensional equations with relatively simple domains of integration and to certain non-linear equations of Hammerstein type (cf. Hammerstein equation).

References

[1]	L.V. Kantorovich, V.I. Krylov, "Approximate methods of higher analysis" , Noordhoff (1958) (Translated from Russian)

References

[a1]	C.T.H. Baker, "The numerical treatment of integral equations" , Clarendon Press (1977) pp. Chapt. 4
[a2]	K.E. Atkinson, "A survey of numerical methods for the solution of Fredholm integral equations of the second kind" , SIAM (1976)
[a3]	I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1981)
[a4]	B.L. Moiseiwitsch, "Integral equations" , Longman (1977)