Degenerate equilibrium position

of a system of ordinary differential equations

A point 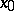for which and for which the matrix has zero eigen values. The most extensively investigated degenerate equilibrium positions are those of two-dimensional systems, for which several methods for studying the behaviour of trajectories in a neighbourhood of this position are available; these include the methods of I. Bendixson [1], [2], [4] and of M. Frommer [3], [4]. Geometric methods of investigation have been recommended in spaces of more than two dimensions; these consist, in essence, in isolating the main terms at the right-hand sides of the equations and demonstrating that the behaviour of the trajectory remains unchanged on passing from the abbreviated to the complete equation [5]. If the mapping 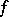is sufficiently often differentiable or analytic, the degree of degeneracy of the equilibrium position may be considered equal to the number of non-degenerate equilibrium positions into which the given degenerate equilibrium position may be subdivided as a result of a change in which is small in the sense of the 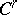-topology.

References

[1]	I. Bendixson, "Sur les courbes définies par des équations différentielles" Acta Math. , 24 (1901) pp. 1–88
[2]	A.A. Andronov, E.A. Leontovich, I.I. Gordon, A.G. Maier, "Qualitative theory of second-order dynamic systems" , Wiley (1973) (Translated from Russian)
[3]	M. Frommer, "Die Integralkurven einer gewöhnlichen Differentialgleichung erster Ordnung in der Umgebung rationaler Unbestimmtheitsstellen" Math. Ann. , 99 (1928) pp. 222–272
[4]	V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian)
[5]	A.A. Bryuno, "Stepwise asymptotic solutions of non-linear systems" Izv. Akad. Nauk SSSR Ser. Mat. , 29 (1965) pp. 329–364 (In Russian)

Comments

See also Frommer method for the study of the behaviour of trajectories in a neighbourhood of an equilibrium position.

References

[a1]	M.W. Hirsch, S. Smale, "Differential equations, dynamical systems, and linear algebra" , Acad. Press (1974)
[a2]	J.K. Hale, "Ordinary differential equations" , Wiley (1980)