Definite kernel
From Encyclopedia of Mathematics
The kernel 
of a linear integral Fredholm operator which satisfies the relation
 |
where 
are points in a Euclidean space, 
is an arbitrary square-integrable function, and 
is its complex conjugate function. Depending on the sign of the inequality, the kernel is said to be, respectively, non-negative (non-negative definite) or non-positive (non-positive definite).
Non-negative (non-positive) is sometimes the name given to a kernel which satisfies, in the domain of integration, the inequality 
(
).
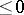Comments
References
| [a1] | A.C. Zaanen, "Linear analysis" , North-Holland (1956) |
| [a2] | K. Jörgens, "Lineare Integraloperatoren" , Teubner (1970) |
How to Cite This Entry:
Definite kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Definite_kernel&oldid=46606
Definite kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Definite_kernel&oldid=46606
This article was adapted from an original article by A.B. Bakushinskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article