Defining equation
determining equation, characteristic equation
An equation associated with a regular singular point  of an ordinary linear differential equation
of an ordinary linear differential equation
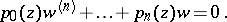 | (1) |
Let
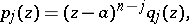 |
where the functions 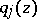 are holomorphic at the point
are holomorphic at the point  and
and 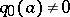 . The defining equation takes the form:
. The defining equation takes the form:
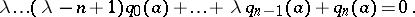 | (2) |
If the roots 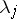 ,
, 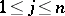 , of equation (2) are such that all differences
, of equation (2) are such that all differences 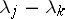 , where
, where 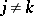 , are not integers, then equation (1) has a fundamental system of solutions of the form
, are not integers, then equation (1) has a fundamental system of solutions of the form
 | (3) |
where the functions  are holomorphic at
are holomorphic at  . Otherwise the coefficients
. Otherwise the coefficients 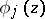 can be polynomials in
can be polynomials in 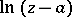 with coefficients holomorphic at
with coefficients holomorphic at  .
.
The defining equation for a system of  equations
equations
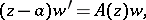 | (4) |
corresponding to the regular singular point  , takes the form
, takes the form
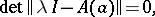 |
where 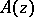 is a matrix-function of order
is a matrix-function of order 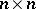 , holomorphic at
, holomorphic at  and
and 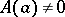 . If all differences
. If all differences 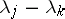 , where
, where 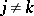 , are not integers, where the
, are not integers, where the  are the eigen values of
are the eigen values of 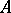 , then the system (4) has a fundamental system of solutions of the form (3), where
, then the system (4) has a fundamental system of solutions of the form (3), where 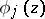 are vector-functions holomorphic at
are vector-functions holomorphic at  ; otherwise, the vector-functions
; otherwise, the vector-functions 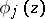 can be polynomials in
can be polynomials in 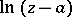 with coefficients which are vector-functions holomorphic at
with coefficients which are vector-functions holomorphic at  .
.
In another sense, the term "determining equation" is used in research on transformation groups admitted by ordinary partial differential equations (see [3]).
References
| [1] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) |
| [2] | E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1971) |
| [3] | L.V. [L.V. Ovsyannikov] Ovsiannikov, "Group analysis of differential equations" , Acad. Press (1982) (Translated from Russian) |
Comments
A defining equation is more commonly called an indicial equation.
Defining equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Defining_equation&oldid=46604