Dedekind completion
of a Riesz space
A Riesz space is called Dedekind complete if every non-empty subset that is bounded from below (respectively, above) has an infimum (respectively, supremum). A Dedekind-complete Riesz space is automatically Archimedean. Hence, so are its Riesz subspaces.
Given an Archimedean Riesz space 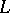 , a Dedekind completion of
, a Dedekind completion of 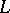 is a pair
is a pair 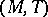 where
where 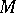 is a Riesz space and
is a Riesz space and  is a mapping such that
is a mapping such that
1) 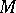 is Dedekind complete;
is Dedekind complete;
2) 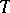 is a Riesz isomorphism of
is a Riesz isomorphism of 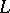 onto a Riesz subspace
onto a Riesz subspace 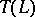 of
of 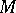 ;
;
3) as a mapping 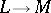 ,
, 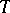 is normal, i.e., it preserves arbitrary suprema and infima;
is normal, i.e., it preserves arbitrary suprema and infima;
4) for all 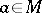 ,
,
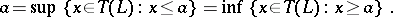 |
Every Archimedean Riesz space 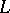 has a Dedekind completion, whose underlying partially ordered set can be obtained from the MacNeille completion (cf. Completion, MacNeille (of a partially ordered set)) of
has a Dedekind completion, whose underlying partially ordered set can be obtained from the MacNeille completion (cf. Completion, MacNeille (of a partially ordered set)) of 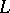 by removing its largest and smallest elements. The Dedekind completion is unique in the following sense. If
by removing its largest and smallest elements. The Dedekind completion is unique in the following sense. If 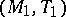 and
and 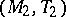 are Dedekind completions of
are Dedekind completions of 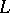 , then there exists a unique Riesz isomorphism
, then there exists a unique Riesz isomorphism 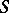 of
of 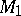 onto
onto 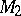 with
with 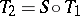 . More generally, if
. More generally, if 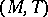 is a Dedekind completion of
is a Dedekind completion of 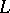 , then every normal Riesz homomorphism of
, then every normal Riesz homomorphism of  into any Dedekind-complete Riesz space
into any Dedekind-complete Riesz space 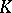 can uniquely be extended to a normal Riesz homomorphism
can uniquely be extended to a normal Riesz homomorphism 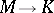 .
.
The Riesz spaces 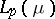 (
(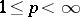 ) are Dedekind complete; so is
) are Dedekind complete; so is 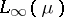 if
if 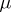 is
is 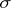 -finite. The space
-finite. The space 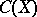 (
(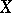 a compact Hausdorff space) is Dedekind complete if and only if
a compact Hausdorff space) is Dedekind complete if and only if  is extremally disconnected (cf. Extremally-disconnected space). There are few non-trivial instances of Riesz spaces whose Dedekind completions are to some extent "understood" . The Dedekind completion of the space
is extremally disconnected (cf. Extremally-disconnected space). There are few non-trivial instances of Riesz spaces whose Dedekind completions are to some extent "understood" . The Dedekind completion of the space  of all converging sequences is
of all converging sequences is 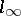 . That of
. That of 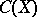 is the quotient
is the quotient 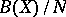 , where
, where 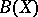 is the space of all bounded Borel functions and
is the space of all bounded Borel functions and 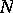 is the ideal of all functions that vanish off meager sets (cf. Category of a set). (In either case, the mapping
is the ideal of all functions that vanish off meager sets (cf. Category of a set). (In either case, the mapping  is obvious.)
is obvious.)
References
| [a1] | E. de Jonge, A. van Rooij, "Introduction to Riesz spaces" , Tracts , 8 , Math. Centre, Amsterdam (1977) |
| [a2] | W. Luxemburg, A.C. Zaanen, "Riesz spaces" , I , North-Holland (1974) |
| [a3] | B.Z. Vulikh, "Introduction to the theory of partially ordered spaces" , Wolters–Noordhoff (1967) (In Russian) |
Dedekind completion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dedekind_completion&oldid=46597