Decreasing function

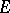A function defined on a set of real numbers such that the condition

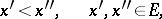implies

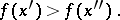Sometimes such a function is called strictly decreasing and the term "decreasing function" is applied to functions satisfying for the indicated values 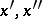only the condition 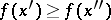(a non-increasing function). Every strictly decreasing function has an inverse function, which is again strictly decreasing. If 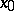is a left-hand (respectively, right-hand) limit point of 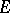, is non-increasing and if the set 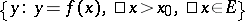is bounded from above (respectively, 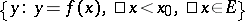is bounded from below), then for 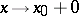(respectively, ), , 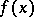has a finite limit; if the given set is not bounded from above (respectively, from below), then 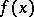has an infinite limit, equal to 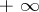(respectively, ).

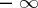Comments

A function 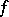such that is decreasing is called increasing (cf. Increasing function).