Decimal approximation of a real number
An approximate representation of a real number by a finite decimal fraction. Any real number  can be written in the form of an infinite decimal fraction
can be written in the form of an infinite decimal fraction
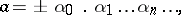 |
where 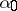 is a non-negative integer,
is a non-negative integer,  is one of the digits
is one of the digits 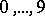 and
and 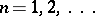 . If one excludes infinite periodic decimal fractions with periods exclusively consisting of nines, one can write any real number in a unique manner as an infinite decimal fraction. Select such a notation for numbers and let
. If one excludes infinite periodic decimal fractions with periods exclusively consisting of nines, one can write any real number in a unique manner as an infinite decimal fraction. Select such a notation for numbers and let 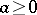 ; then the finite decimal fraction
; then the finite decimal fraction
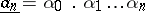 |
(or 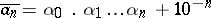 ) is said to be the lower (upper) decimal approximation of order
) is said to be the lower (upper) decimal approximation of order  of
of  . If
. If 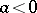 and
and  , then the lower
, then the lower 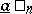 and the upper
and the upper 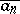 decimal approximations of order
decimal approximations of order  of
of  are defined by
are defined by
 |
The following relations are valid for a decimal approximation of a real number
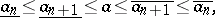 |
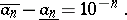 |
It follows that
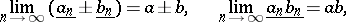 |
and if 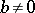 , then
, then  , and upper approximations may be taken instead of lower.
, and upper approximations may be taken instead of lower.
Decimal approximations are used in practice for approximate calculations. The approximate values of the sums  , differences
, differences 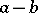 , products
, products  , and quotients
, and quotients 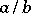 are given, respectively, by
are given, respectively, by  ,
, 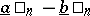 ,
,
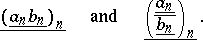 |
As a result of these operations on finite decimal fractions 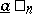 and
and 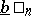 , which have at most
, which have at most  significant figures to the right of the decimal point, one again obtains decimal fractions with at most
significant figures to the right of the decimal point, one again obtains decimal fractions with at most  significant figures to the right of the decimal point. The sought-for result may be obtained to any desired degree of accuracy using these fractions.
significant figures to the right of the decimal point. The sought-for result may be obtained to any desired degree of accuracy using these fractions.
Decimal approximation of a real number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Decimal_approximation_of_a_real_number&oldid=46594