Darboux vector
The vector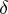 
of the instantaneous axis of rotation around which the natural trihedral of a curve 
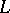is rotating during the uniform movement of a point 
along the curve 
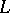. The Darboux vector lies in the rectifying plane of the curve 
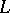and is expressed in terms of the principal normal 
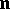and the tangent 
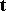of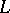 
by the formula
 |
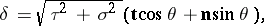where 
and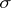 
are the curvature and the torsion of 
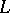and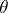 
is the angle between the Darboux vector and the tangent to 
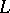. The Frénet formulas may be written with the aid of the Darboux vector as follows:
 |
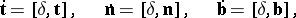where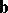 
is the binormal of 
.
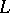G. Darboux [1] was the first to point out the geometric significance of the Darboux vector for the natural trihedral of a space curve.
References
| [1] | G. Darboux, "Leçons sur la théorie générale des surfaces et ses applications géométriques du calcul infinitésimal" , 1 , Gauthier-Villars (1887) pp. 1–18 |
| [2] | V.F. Kagan, "Foundations of the theory of surfaces in a tensor setting" , 1 , Moscow-Leningrad (1947) (In Russian) |
Comments
The natural trihedral (a name used by S. Sternberg [a1]) is commonly called Frénet frame (also Frénet trihedron).
References
| [a1] | S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) |
| [a2] | W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973) |
Darboux vector. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Darboux_vector&oldid=46584