Darboux trihedron
From Encyclopedia of Mathematics
A trihedron associated with a point on a surface and defined by a triple of vectors, given by the normal unit vector  to the surface and two mutually orthogonal principal unit tangent vectors
to the surface and two mutually orthogonal principal unit tangent vectors  and
and  to the surface such that
to the surface such that
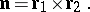 |
The properties of the surface can be described in terms of displacement of the Darboux trihedron when its base point describes the surface. A systematic use of the Darboux trihedron in the study of surfaces led G. Darboux [1] to the moving-frame method.
References
| [1] | G. Darboux, "Leçons sur la théorie générale des surfaces et ses applications géométriques du calcul infinitésimal" , 1 , Gauthier-Villars (1887) |
Comments
A Darboux trihedron is also called a Darboux frame. It is also introduced in affine differential geometry, cf. [a1].
References
| [a1] | H.W. Guggenheimer, "Differential geometry" , McGraw-Hill (1963) |
How to Cite This Entry:
Darboux trihedron. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Darboux_trihedron&oldid=46583
Darboux trihedron. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Darboux_trihedron&oldid=46583
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article