Cylindrical measure

A cylindrical measure in measure theory on topological vector spaces is a finitely-additive measure defined on the algebra of cylinder sets in a topological vector space , that is, sets of the form

(*)

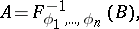where 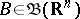— the Borel -algebra of subsets of the space , ; are linear functionals on , and 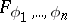is the mapping

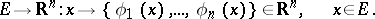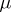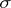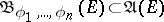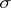Here it is assumed that the restriction of to any -subalgebra of sets of the form (*) with a fixed collection of functionals is a -additive measure on (other names are pre-measure, quasi-measure).

In the theory of functions of several real variables a cylindrical measure is a special case of the Hausdorff measure, defined on the Borel 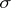-algebra of the space by means of the formula

where the lower bound is taken over all finite or countable coverings of a set by cylinders 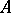with spherical bases and axes parallel to the -st coordinate axis in ; here is the -dimensional volume of an axial section of the cylinder . When 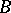is the graph of a continuous function of variables defined in a domain :

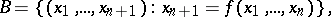then 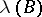is the same as the so-called -dimensional variation of .

References

[1]	I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , 4 , Acad. Press (1968) (Translated from Russian)
[2]	A.G. Vitushkin, "On higher-dimensional variations" , Moscow (1955) (In Russian)

Comments

Concerning the -dimensional variation of a function see Variation of a function.

References

[a1]	L. Schwartz, "Radon measures on arbitrary topological spaces and cylindrical measures" , Oxford Univ. Press (1973)