Covariance of the number of solutions

A concept in the dispersion method introduced for the comparison of the number of solutions of the equations

(1)

and

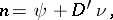(2)

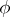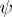where and belong to certain sequences of positive integers, 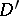runs through some given system of intervals on the real axis

and runs through a system of intervals on the real axis

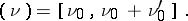Let

then the dispersion of the difference of the solutions of (1) and (2) is

where

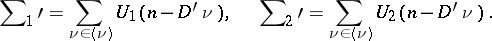Applying an idea of I.M. Vinogradov on smoothing double sums, one can extend the summation over 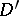to all of 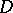in . This can only increase the dispersion; thus

where

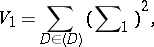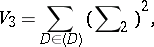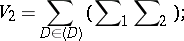here

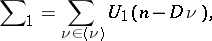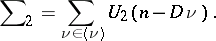In analogy with probability-theoretic concepts, 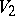is called the covariance of the number of solutions of (1) and (2). An asymptotic estimate of 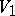, 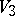and the covariance 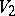shows that the dispersion 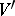is relatively small, and this is essential in considering additive problems that lead to equations (1) and (2).

References

[1]	Yu.V. Linnik, "The dispersion method in binary additive problems" , Amer. Math. Soc. (1963) (Translated from Russian)

Comments

See also Circle method.