Conormal
From Encyclopedia of Mathematics
A term used in the theory of boundary value problems for partial differential equations (cf. Boundary value problem, partial differential equations). Let 
be the outward normal at a point 
to a smooth surface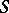 
situated in a Euclidean space 
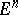with coordinates 
, and let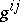 
be a contravariant continuous tensor, usually representing the coefficients of some second-order (elliptic) differential operator 
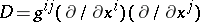. Then the conormal (with respect to 
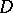) is the vector
 |
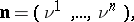where 
. In other words, the conormal is the contravariant description (in the space with metric defined by the tensor inverse to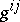 
) of the normal covariant vector 
to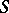 
(in the space with Euclidean metric).
References
| [1] | A.V. Bitsadze, "Equations of mathematical physics" , MIR (1980) (Translated from Russian) |
| [2] | C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian) |
Comments
References
| [a1] | A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) |
How to Cite This Entry:
Conormal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conormal&oldid=46480
Conormal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conormal&oldid=46480
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article