Connection object

A differential-geometric object on a smooth principal fibre bundle that is used to define a horizontal distribution of a connection in . Let be the bundle of all tangent frames to such that the first vectors are tangent to the corresponding fibre, and are generated by basis elements in the Lie algebra of the structure group of , . A connection object then consists of functions on such that the subspace of 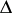is spanned by the vectors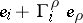 . 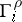Furthermore, the must satisfy the following conditions on :

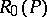(1)

They are expressed by using the 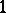-forms on that occur in the structure equations for the forms 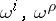given by the co-basis dual to ;

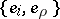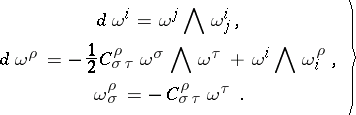(2)

A connection object also defines a corresponding connection form , given by the relation , and its curvature form , given by the formulas:

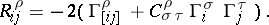For example, let 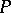be the space of affine tangent frames of an -dimensional smooth manifold . Then the second equation in (2) has the form

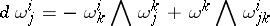and (1) reduces to

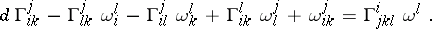Under parallel displacement one must have 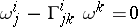. If a local chart is chosen in 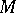, and if in its domain one makes the transition to the natural frame of the chart, i.e. , then the parallel displacement is defined by . The classical definition of a connection object of an affine connection on is given by the set of functions 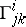defined on the domains of the charts such that under transition to the coordinates of another chart these functions are transformed according to the formulas

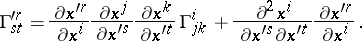Here this follows from the condition of invariance under displacement.