Conjugate class of functions

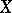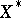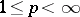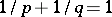A concept in the theory of functions which is a concrete instance of duality in functions spaces. Thus, if a class of functions is regarded as a Banach space or a topological vector space, then the conjugate class is defined as the class of functions isometrically isomorphic to the dual space . For example, when and , there is an isometric isomorphism between the spaces 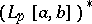and 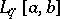, under which corresponding elements 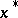and 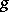are related by

If one considers some class 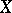of 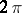-periodic summable functions on 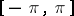, then the conjugate class is defined to be the class of functions conjugate to the functions in 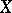. For example, the class conjugate to 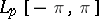(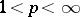) coincides with the class of functions 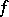in for which

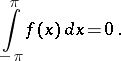The class conjugate to , , 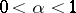coincides with the class of functions in 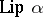for which .

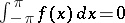References

[1]	M. Fréchet, C.R. Acad. Sci. , 144 (1907) pp. 1414–1416
[2]	F. Riesz, C.R. Acad. Sci. , 144 (1907) pp. 1409–1411
[3]	I. [I. Privalov] Priwaloff, Bull. Soc. Math. France , 44 (1916) pp. 100–103
[4]	N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian)
[5]	N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958)