Congruence with several variables
A congruence
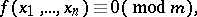 | (1) |
where 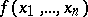 is a polynomial in
is a polynomial in 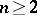 variables with integer rational coefficients not all of which are divisible by
variables with integer rational coefficients not all of which are divisible by 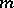 . The solvability of this congruence modulo
. The solvability of this congruence modulo 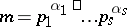 , where
, where 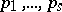 are different prime numbers, is equivalent to the solvability of the congruences
are different prime numbers, is equivalent to the solvability of the congruences
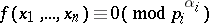 | (2) |
for all 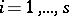 . The number
. The number 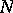 of solutions of (1) is then equal to the product
of solutions of (1) is then equal to the product  , where
, where 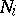 is the number of solutions of (2). Thus, when studying congruences of the form (1) it is sufficient to confine oneself to moduli that are powers of prime numbers.
is the number of solutions of (2). Thus, when studying congruences of the form (1) it is sufficient to confine oneself to moduli that are powers of prime numbers.
For a congruence
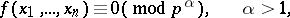 | (3) |
to be solvable, it is necessary that the congruence
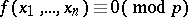 | (4) |
modulo a prime number  be solvable. In non-degenerate cases, the solvability of (4) is also a sufficient condition for the solvability of (3). More precisely, the following statement is correct: Every solution
be solvable. In non-degenerate cases, the solvability of (4) is also a sufficient condition for the solvability of (3). More precisely, the following statement is correct: Every solution 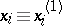 (
(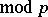 ) of (4) such that
) of (4) such that 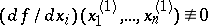 (
(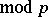 ) for at least one
) for at least one 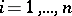 , generates
, generates 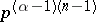 solutions
solutions 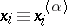 (
( ) of (3), whereby
) of (3), whereby 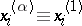 (
(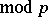 ) when
) when 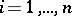 .
.
Thus, in the non-degenerate case, the question of the number of solutions of the congruence (1) modulo a composite number 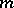 reduces to the question of the number of solutions of congruences of the form (4) modulo the prime numbers
reduces to the question of the number of solutions of congruences of the form (4) modulo the prime numbers 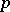 that divide
that divide 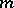 . If
. If  is an absolutely-irreducible polynomial with integer rational coefficients, then for the number
is an absolutely-irreducible polynomial with integer rational coefficients, then for the number  of solutions of (4), the estimate
of solutions of (4), the estimate
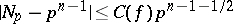 |
holds, where the constant 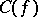 depends only on
depends only on 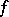 and does not depend on
and does not depend on 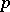 . It follows from this estimate that the congruence (4) is solvable for all prime numbers
. It follows from this estimate that the congruence (4) is solvable for all prime numbers 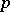 that are larger than a certain effectively-calculable constant
that are larger than a certain effectively-calculable constant 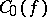 , depending on the given polynomial
, depending on the given polynomial 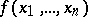 (see also Congruence modulo a prime number). A stronger result in this question has been obtained by P. Deligne [3].
(see also Congruence modulo a prime number). A stronger result in this question has been obtained by P. Deligne [3].
References
| [1] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) |
| [2] | H. Hasse, "Zahlentheorie" , Akademie Verlag (1963) |
| [3] | P. Deligne, "La conjecture de Weil I" Publ. Math. IHES , 43 (1974) pp. 273–307 |
Comments
See also Congruence equation for more information. A polynomial  over
over  is absolutely irreducible if it is still irreducible over any (algebraic) field extension of
is absolutely irreducible if it is still irreducible over any (algebraic) field extension of 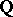 .
.
Congruence with several variables. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Congruence_with_several_variables&oldid=46464