Congruence modulo a double modulus
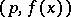, congruence relative to a double modulus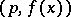 
A relation between integral polynomials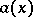 
and 
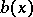of the form
 |
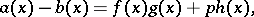where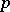 
is a prime number, while 
, 
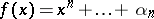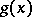and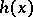 
are polynomials with integer rational coefficients. In other words, the polynomials 
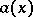and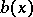 
with rational coefficients are called congruent modulo the double modulus 
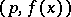if the difference 
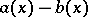between them is divisible by 
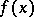modulo 
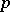. In order to denote the congruence of 
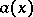and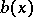 
modulo the double modulus 
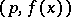, the symbol
 |
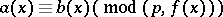is used. This symbol, as well as the actual concept of a congruence modulo a double modulus, was introduced by R. Dedekind.
A congruence modulo a double modulus is an equivalence relation on the set of all integral polynomials and, consequently, divides this set into non-intersecting classes, called residue classes modulo the double modulus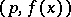 
. Since every polynomial 
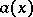is congruent modulo the double modulus 
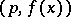to one and only one polynomial of the form
 |
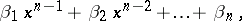where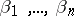 
run independently of each other through a complete residue system modulo 
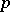, there are exactly 
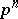residue classes modulo 
.
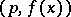Congruences modulo a double modulus can be added, subtracted and multiplied in the same way as normal congruences. These operations induce similar operations on the residue classes modulo a double modulus, thus transforming the set of residue classes into a commutative ring.
The ring of residue classes modulo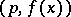 
is the quotient ring of the ring of polynomials 
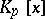with coefficients from a finite prime field 
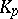by the ideal 
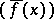generated by the polynomial 
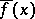, obtained from 
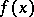by reduction modulo 
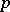. In particular, if 
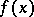is irreducible modulo 
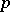, then 
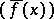is a maximal ideal in 
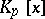, and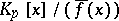 
is a field consisting of 
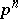elements (an extension of degree n of the prime field 
).
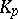If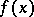 
is irreducible modulo 
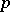, then for congruences modulo a double modulus, the analogue of the Fermat little theorem holds:
 |
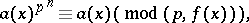as does the Lagrange theorem: The congruence
 |
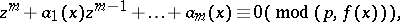the coefficients of which are integral polynomials, has not more than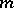 
incongruent solutions modulo 
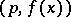. From these theorems it is possible to deduce that
 |
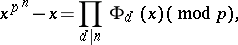where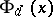 
is the product of all possible different, normalized (i.e. with leading coefficient 1), irreducible polynomials modulo 
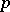of degree 
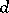. If the number of different, normalized, irreducible polynomials modulo 
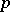of degree 
is denoted by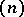 
, then
 |
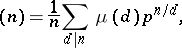where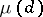 
is the Möbius function and, in particular, 
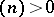for any natural number 
. Consequently there exists, for any integer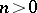 
, a finite field 
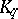consisting of 
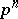elements that is an extension of degree 
of the residue field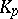 
modulo the prime number 
.
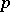References
| [1] | B.A. Venkov, "Elementary number theory" , Wolters-Noordhoff (1970) (Translated from Russian) |
Comments
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapts. 5; 7; 8 |
Congruence modulo a double modulus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Congruence_modulo_a_double_modulus&oldid=46462