Conformally-invariant metric
on a Riemann surface 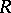
A rule that associates with each local parameter  , mapping a parameter neighbourhood
, mapping a parameter neighbourhood 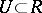 into the closed complex plane
into the closed complex plane 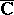 (
(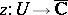 ), a real-valued function
), a real-valued function
 |
such that for all local parameters 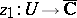 and
and 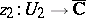 for which the intersection
for which the intersection  is not empty, the following relation holds:
is not empty, the following relation holds:
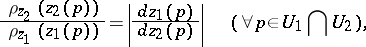 |
where  is the image of
is the image of 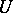 in
in 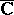 under
under  . A conformally-invariant metric is often denoted by the symbol
. A conformally-invariant metric is often denoted by the symbol  , to which the indicated invariance with respect to the choice of the local parameter
, to which the indicated invariance with respect to the choice of the local parameter  is attributed.
is attributed.
Every linear differential 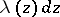 (or quadratic differential
(or quadratic differential  ) induces a conformally-invariant metric,
) induces a conformally-invariant metric, 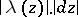 (or
(or  ). The notion of a conformally-invariant metric, being a very general form of defining conformal invariants, enables one to introduce that of the length of curves on
). The notion of a conformally-invariant metric, being a very general form of defining conformal invariants, enables one to introduce that of the length of curves on  as well as the notion of the extremal length and the modulus of families of curves (see Extremal metric, method of the, and also [1]). The definition of a conformally-invariant metric can be carried over to Riemann varieties of arbitrary dimension.
as well as the notion of the extremal length and the modulus of families of curves (see Extremal metric, method of the, and also [1]). The definition of a conformally-invariant metric can be carried over to Riemann varieties of arbitrary dimension.
References
| [1] | J.J. Jenkins, "Univalent functions and conformal mapping" , Springer (1958) |
| [2] | M. Schiffer, D.C. Spencer, "Functionals of finite Riemann surfaces" , Princeton Univ. Press (1954) |
| [3a] | L.V. Ahlfors, "The complex analytic structure of the space of closed Riemann surfaces" R. Nevanlinna (ed.) et al. (ed.) , Analytic functions , Princeton Univ. Press (1960) pp. 45–66 |
| [3b] | L.V. Ahlfors, "On quasiconformal mappings" J. d'Anal. Math. , 3 (1954) pp. 1–58 |
| [3c] | L.V. Ahlfors, "Correction to "On quasiconformal mappings" " J. d'Anal. Math. , 3 (1954) pp. 207–208 |
| [3d] | L. Bers, "Quasi-conformal mappings and Teichmüller's theorem" R. Nevanlinna (ed.) et al. (ed.) , Analytic functions , Princeton Univ. Press (1960) pp. 89–119 |
| [3e] | L. Bers, "Spaces of Riemann surfaces" J.A. Todd (ed.) , Proc. Internat. Congress Mathematicians (Edinburgh, 1958) , Cambridge Univ. Press (1960) pp. 349–361 |
| [3f] | L. Bers, "Simultaneous uniformization" Bull. Amer. Math. Soc. , 66 (1960) pp. 94–97 |
| [3g] | L. Bers, "Holomorphic differentials as functions of moduli" Bull. Amer. Math. Soc. , 67 (1961) pp. 206–210 |
Comments
References
| [a1] | L.V. Ahlfors, "Lectures on quasiconformal mappings" , v. Nostrand (1966) |
Conformally-invariant metric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conformally-invariant_metric&oldid=46460