Conformal measure

The original definition of a conformal measure (or density) is due to S.J. Patterson [a2] in the case of a Fuchsian group 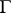acting on the hyperbolic space 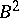(cf. Poincaré model). Its definition carries over to any dimension (D. Sullivan, [a4]):

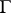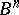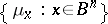Let be a discrete group of transformations acting on the hyperbolic space of dimension . A family of probability measures (cf. Probability measure) supported on the limit set 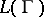is called 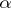-conformal if for every 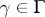and every 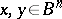the measures 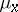and 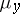are equivalent with Radon–Nikodým derivative (cf. also Radon–Nikodým theorem)

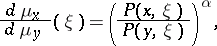where 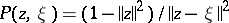denotes the Poisson kernel (cf. Poisson integral).

Conformality of the measure can be described by restricting to 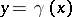, where 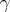is any Möbius function leaving 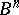invariant. In this case the definition reads:

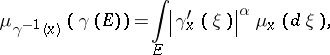where 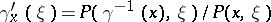and 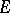is any measurable set. If 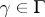and , then 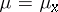is a conformal measure in the following sense (see [a1]).

Let 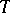be a measurable transformation (cf. Measurable mapping) acting on the measure space 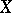with 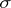-algebra 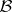. A measure 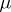is called conformal for the function 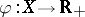if for every set 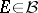on which 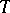acts as a measurable isomorphism,

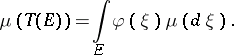Thus, 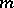is conformal for 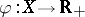if and only if the Jacobian of 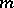under 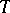is given by 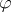. The Frobenius–Perron operator 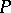can be defined as the restriction to 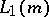of the dual operator on 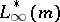, , 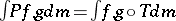and it satisfies 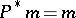. In many examples 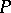can be written explicitly in the form

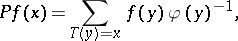and this representation permits the application of Ruelle's thermodynamic formalism [a3]. The importance of the notion of a conformal measure can be seen from this.

Besides its use in the ergodic theory of dynamical systems and statistical mechanics (including discrete groups and geodesic flows), it allows one to study geometric and number-theoretic problems like fractal dimensions, Diophantine approximations and recurrence.

References

[a1]	M. Denker, M. Urbański, "On the existence of conformal measures" Trans. Amer. Math. Soc. , 328 (1991) pp. 563–587
[a2]	S.J. Patterson, "The limit set of a Fuchsian group" Acta Math. , 136 (1976) pp. 241–273
[a3]	D. Sullivan, "The density at infinity of a discrete group of hyperbolic motions" IHES Publ. Math. , 50 (1979) pp. 171–202
[a4]	D. Ruelle, "Thermodynamic formalism" , Encycl. Math. Appl. , 5 , Addison-Wesley (1976)