Condensing operator
From Encyclopedia of Mathematics
An operator 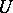 , generally non-linear, defined on the set
, generally non-linear, defined on the set 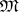 of all subsets of a set
of all subsets of a set 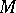 in a normed vector space
in a normed vector space  , with values in a normed vector space
, with values in a normed vector space 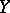 , such that
, such that 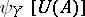 — the measure of non-compactness of the set
— the measure of non-compactness of the set 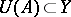 — is less than the measure of non-compactness
— is less than the measure of non-compactness 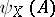 for any non-compact set
for any non-compact set 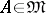 . Here, the measures of non-compactness may be the same in both cases or different. For example, as
. Here, the measures of non-compactness may be the same in both cases or different. For example, as 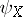 and
and 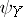 one may take the Kuratowski measure of non-compactness:
one may take the Kuratowski measure of non-compactness: 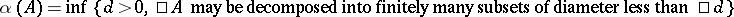 .
.
For a continuous condensing operator many constructions and facts of the theory of completely-continuous operators can be carried over, for instance, the rotation of contracting vector fields, the fixed-point principle of contraction operators, etc.
References
| [1] | B.N. Sadovskii, "Limit-compact and condensing operators" Russian Math. Surveys , 27 (1972) pp. 85–155 Uspekhi Mat. Nauk , 27 : 1 (1972) pp. 81–146 |
| [2] | C. Kuratowski, "Sur les espaces complets" Fund. Math. , 15 (1930) pp. 301–309 |
How to Cite This Entry:
Condensing operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Condensing_operator&oldid=46439
Condensing operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Condensing_operator&oldid=46439
This article was adapted from an original article by V.I. Sobolev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article