Concave and convex operators
Non-linear operators in semi-ordered spaces that are analogues of concave and convex functions of a real variable.
A non-linear operator 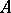 that is positive on a cone
that is positive on a cone 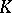 in a Banach space is said to be concave (more exactly,
in a Banach space is said to be concave (more exactly, 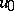 -concave on
-concave on 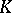 ) if
) if
1) the following inequalities are valid for any non-zero 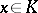 :
:
 |
where 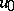 is some fixed non-zero element of
is some fixed non-zero element of 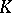 and
and 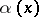 and
and 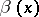 are positive scalar functions;
are positive scalar functions;
2) for each 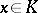 such that
such that
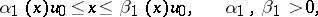 |
the following relations are valid:
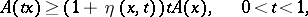 | (*) |
where 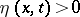 .
.
In a similar manner, an operator  is said to be convex (more exactly,
is said to be convex (more exactly, 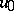 -convex on
-convex on 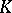 ) if conditions 1) and 2) are met but the inequality (*) is replaced by the opposite inequality, with a function
) if conditions 1) and 2) are met but the inequality (*) is replaced by the opposite inequality, with a function 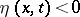 .
.
A typical example is Urysohn's integral operator
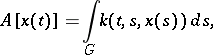 |
the concavity and convexity of which is ensured by, respectively, the concavity and convexity of the scalar function 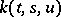 with respect to the variable
with respect to the variable  . Concavity of an operator means that it contains only "weak" non-linearities — the values of the operator on the elements of the cone increase "slowly" with the increase in the norms of the elements. Convexity of an operator means, as a rule, that it contains "strong" non-linearities. For this reason equations involving concave operators differ in many respects from equations involving convex operators; the properties of the former resemble the corresponding scalar equations, unlike the latter for which the theorem on the uniqueness of a positive solution is not valid.
. Concavity of an operator means that it contains only "weak" non-linearities — the values of the operator on the elements of the cone increase "slowly" with the increase in the norms of the elements. Convexity of an operator means, as a rule, that it contains "strong" non-linearities. For this reason equations involving concave operators differ in many respects from equations involving convex operators; the properties of the former resemble the corresponding scalar equations, unlike the latter for which the theorem on the uniqueness of a positive solution is not valid.
References
| [1] | M.A. Krasnosel'skii, P.P. Zabreiko, "Geometric methods of non-linear analysis" , Springer (1983) (Translated from Russian) |
Concave and convex operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Concave_and_convex_operators&oldid=46437