Complex structure
A complex structure on a real vector space  is the structure of a complex vector space on
is the structure of a complex vector space on  that is compatible with the original real structure. The complex structure on
that is compatible with the original real structure. The complex structure on  is completely determined by the operator of multiplication by the number
is completely determined by the operator of multiplication by the number  , the role of which can be taken by an arbitrary linear transformation
, the role of which can be taken by an arbitrary linear transformation  satisfying
satisfying  , where
, where  is the identity. Therefore, a transformation of this type is often called a complex structure on
is the identity. Therefore, a transformation of this type is often called a complex structure on  . If
. If  is endowed with a complex structure and
is endowed with a complex structure and  is a basis of this space over
is a basis of this space over  , then
, then  forms a basis of it over
forms a basis of it over 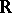 , so that
, so that 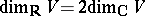 . If
. If  is a complex structure on
is a complex structure on 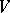 then the complexification
then the complexification 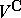 of
of  decomposes into a direct sum
decomposes into a direct sum  , where
, where 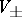 are the eigen spaces of the transformation
are the eigen spaces of the transformation 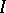 extended to
extended to  corresponding to the eigen values
corresponding to the eigen values 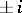 , and
, and  . Conversely, each complex subspace
. Conversely, each complex subspace 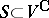 such that
such that  determines a complex structure on
determines a complex structure on  for which
for which 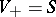 .
.
Any two complex structures on a 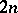 -dimensional real space
-dimensional real space 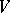 can be mapped into each other by some automorphism of
can be mapped into each other by some automorphism of  . The set of all complex structures on
. The set of all complex structures on  is thus a homogeneous space of the group
is thus a homogeneous space of the group  and is identified with the quotient space
and is identified with the quotient space  , where
, where  is the subgroup of non-singular matrices of the form
is the subgroup of non-singular matrices of the form
 |
A complex structure on a differentiable manifold is the structure of a complex-analytic manifold (cf. Analytic manifold). If 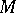 is a differentiable manifold, then a complex structure on
is a differentiable manifold, then a complex structure on  is a complex-analytic atlas on
is a complex-analytic atlas on 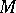 that is compatible with the real differentiable atlas defined on
that is compatible with the real differentiable atlas defined on  . Here
. Here  . A complex structure on
. A complex structure on 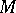 induces a complex structure on each tangent space
induces a complex structure on each tangent space 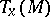 , and therefore induces on
, and therefore induces on  an almost-complex structure which completely determines it.
an almost-complex structure which completely determines it.
References
| [1] | A. Lichnerowicz, "Global theory of connections and holonomy groups" , Noordhoff (1976) (Translated from French) |
| [2] | R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) |
Complex structure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complex_structure&oldid=46432