Complex of lines

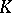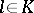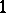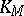A set of straight lines in -dimensional (projective, affine, Euclidean) space depending on three parameters. A straight line is called a ray of the complex. Through each point of the ambient space there passes a -parameter family of rays of the complex, called the cone of and denoted by . A complex of lines defines a correspondence between the points of a ray of the complex and the planes passing through this ray: Corresponding to each point 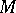of the ray 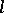is the plane 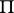tangent to the cone 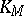at the point . This correspondence is called the normal correlation. Each plane of the space contains a 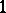-parameter family of rays of the complex enveloping plane curve . 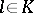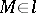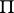By a centre of inflection of a ray one means a point at which the curve of the plane corresponding to the point in the normal correlation has a cusp. On each ray of a complex there are, in general, four centres of inflection. A point of tangency of a ruled surface of a complex is a point on a generator of it at which the tangent plane of the surface is the same as the plane 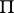corresponding to the point 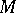in the normal correlation. On every ruled surface of a complex there are, in general, precisely two points of tangency. The lines described by these points are called lines of tangency of the ruled surface. The principal surfaces of a complex are the ruled surfaces for which the lines of tangency are asymptotic lines of them. A projective classification of complexes can be realized in terms of the multiplicity of the centres of inflection of their rays.

In Euclidean space, on each ray 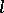one has an invariant point 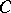(the centre of the ray) at which the vector of the normal to the plane 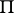that corresponds to the point 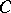in the normal correlation is orthogonal to the normal to the plane 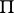corresponding to the ideal point of 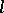. Examples of a complex are: a special complex, i.e. the set of all tangents to a given surface; a linear complex, defined by a linear homogeneous equation with respect to the Grassmann coordinates of the rays of the complex; and a special linear complex, i.e. the set of straight lines of three-dimensional space that intersect a given straight line.

Besides a complex of lines it is possible to consider a complex (a -parameter family) of planes, conics, quadrics, and other figures (see Manifold of figures (lines, surfaces, spheres,...)).

References

[1]	S.P. Finikov, "Theorie der Kongruenzen" , Akademie Verlag (1959) (Translated from Russian)
[2]	N.I. Kovantsov, "Theory of complexes" , Kiev (1963) (In Russian)