Complex (in homological algebra)

One of the basic concepts of homological algebra. Let be an Abelian category. A graded object is a sequence of objects in . A sequence of morphisms is called a morphism of graded objects. One defines the object by setting . A morphism of graded objects 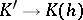is called a morphism of degree from into . A graded object is said to be positive if for all , bounded from below if 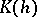is positive for some and finite or bounded if for all but a finite number of integers . A chain complex in a category 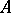consists of a graded object and a morphism of degree such that . 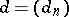More precisely: , where and 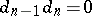for any . A morphism of chain complexes

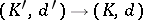is a morphism of graded objects for which . A cochain complex is defined in a dual manner (as a graded object with a morphism of degree ).

Most frequently, complexes are considered in categories of Abelian groups, modules or sheaves of Abelian groups on a topological space. Thus, a complex of Abelian groups is a graded differential group the differential of which has degree 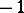or .

Associated with each complex 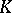are the three graded objects:

the boundaries , where ;

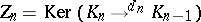the cycles , where ; and

the -dimensional homology objects (classes) 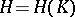, where (see Homology of a complex).

For a cochain complex, the analogous objects are called coboundaries, cocycles and cohomology objects (notations 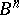, and 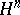, respectively).

If 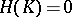, then the complex is said to be acyclic.

A morphism of complexes induces morphisms

and hence a homology or cohomology morphism

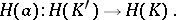Two morphisms are said to be homotopic (denoted by 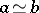) if there is a morphism 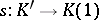(or for cochain complexes) of graded objects (called a homotopy), such that

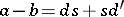(which implies that ). A complex is said to be contractible if , in which case the complex 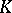is acyclic.

If is an exact sequence of complexes, then there exists a connecting morphism of degree () that is natural with respect to morphisms of exact sequences and is such that the long homology sequence (that is, the sequence

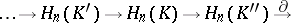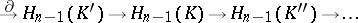for a chain complex, and the sequence

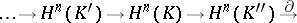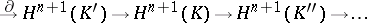for a cochain complex) is exact.

The cone of a morphism 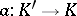of chain complexes is the complex defined as follows:

with

The direct sum decomposition of the complex leads to an exact sequence of complexes

for which the associated long homology sequence is isomorphic to the sequence

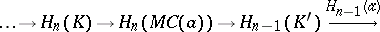Hence the chain complex is acyclic if and only if is an isomorphism. Analogous notions and facts hold for cochain complexes.

References

[1]	H. Bass, "Algebraic 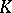-theory" , Benjamin (1968)
[2]	H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956)
[3]	P.J. Hilton, U. Stammbach, "A course in homological algebra" , Springer (1971)
[4]	S. MacLane, "Homology" , Springer (1963)