Completion of a uniform space
A separated complete uniform space 
for which there exists a uniformly-continuous mapping 
such that for any uniformly-continuous mapping 
from 
into a separated complete uniform space 
there exists a unique uniformly-continuous mapping 
with 
. The subspace 
is dense in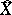 
and the image of entourages in 
under 
are entourages in 
; their closures in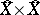 
constitute a fundamental system of entourages in 
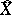. If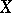 
is separated, then 
is injective (this allows one to identify 
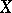with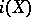 
). The separated completion of a subspace 
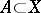is isomorphic to the closure of 
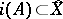. The separated completion of a product of uniform spaces is isomorphic to the product of the separated completions of the spaces occurring as factors in the product.
The proof of the existence of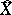 
generalizes in fact Cantor's construction of the set of real numbers from the set of rational numbers.
References
| [1] | N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French) |
Completion of a uniform space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Completion_of_a_uniform_space&oldid=46426