Compatible distributions

projective system of probability measures, consistent system of probability measures, consistent system of distributions

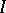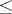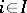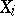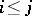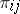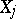A concept in probability theory and measure theory. For the most common and most important case of a product of spaces, see the article Measure. A more general construction is given below. 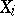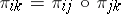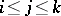Let be an index set with a pre-order relation filtering to the right; suppose one is given a projective system of sets: For every there is a set and for every pair of indices there is a mapping of into such that for ; let 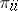be the identity mapping on 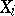for every 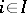. 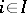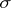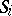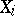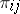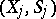It is further assumed that for each there is a -algebra of subsets of such that for the mapping of into 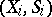is measurable. Finally, let 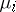be a given distribution (or, more generally, a measure) on 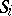, for every 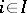. The system of distributions (measures) 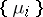is called compatible (or consistent, or a projective system of distributions (measures)) if whenever 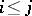. Under certain additional conditions on the projective limit 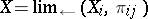, there is a measure 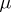(the projective limit of the projective system ) such that if 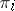is the canonical projection of 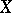to 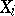, then 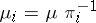for all .

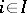References

[1]	A.N. Kolmogorov, "Foundations of the theory of probability" , Chelsea, reprint (1950) (Translated from Russian)
[2]	S. Bochner, "Harmonic analysis and the theory of probability" , Univ. California Press (1955)
[3]	M. Metivier, "Limites projectives de measures. Martingales. Applications" Ann. Mat. Pura Appl. , 63 (1963) pp. 225–352
[4]	N. Bourbaki, "Elements of mathematics. Integration" , Addison-Wesley (1975) pp. Chapt.6;7;8 (Translated from French)

Comments

A partial order or pre-order relati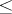on on 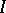is said to filter to the right if for every there is a 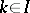such that 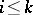and 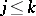. The projective limit measure exists if, for instance, the 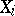are all compact spaces, the 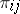are all surjective and the family of norms 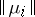is bounded, where 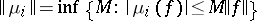, , 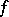continuous of compact support. It also exists if the 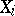are compact, 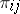surjective, and the 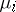are positive measures; then 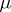is positive and 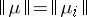for all .

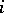The concept of consistency (compatibility) of distributions (or measures) is of special importance in the construction of stochastic processes (cf. Stochastic process; Joint distribution).