Comparison of topologies

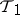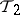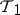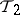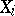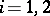An order relation on the set of all topologies on one and the same set . A topology majorizes a topology (or is not weaker than ), if the identity mapping , where is the set with the topology , , is continuous. Moreover, if 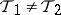, then 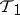is stronger than 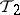(or is weaker than ).

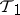The following statements are equivalent:

1) 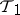majorizes .

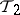2) For any 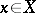, every neighbourhood of in the topology 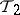is a neighbourhood of in the topology .

3) For any 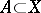, the closure of in 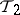contains the closure of in .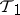

4) Every set from , closed in 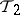, is also closed in .

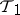5) Every set that is open in 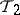is open in .

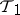In the ordered set of topologies on , the discrete topology is the strongest, while the topology whose only closed sets are 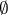and is the weakest. Figuratively speaking, the stronger the topology, the more open sets, closed sets and neighbourhoods there are in ; the stronger the topology, the smaller the closure of a set (and the larger its interior) and the smaller the number of everywhere-dense sets.