Circular symmetrization
From Encyclopedia of Mathematics
A geometrical transformation of an open (closed) set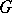 
in the plane, relative to a ray 
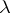emanating from a point 
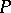, onto a set 
in the same plane defined as follows: 1) the intersection of 
with some circle with centre at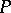 
is either empty or is the entire circle, depending on whether the intersection of 
with the same circle is empty or the entire circle, respectively; and 2) if the intersection of 
with a circle with centre at 
has angular Lebesgue measure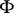 
, then the intersection of 
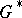with the same circle is an open (closed) arc intersecting 
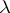, symmetric about 
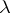and visible from 
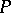at angle 
.
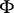The above definition carries over in a natural way to the three-dimensional case (symmetrization relative to a half-plane). See also Symmetrization.
References
| [1] | G. Pólya, G. Szegö, "Isoperimetric inequalities in mathematical physics" , Princeton Univ. Press (1951) |
| [2] | W.K. Hayman, "Multivalent functions" , Cambridge Univ. Press (1958) |
| [3] | J.A. Jenkins, "Univalent functions and conformal mapping" , Springer (1958) |
How to Cite This Entry:
Circular symmetrization. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Circular_symmetrization&oldid=46346
Circular symmetrization. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Circular_symmetrization&oldid=46346
This article was adapted from an original article by I.P. Mityuk (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article