Christoffel numbers
From Encyclopedia of Mathematics
Christoffel coefficients
The coefficients 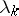 of a quadrature formula
of a quadrature formula
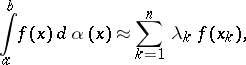 |
which is exact for algebraic polynomials of degrees 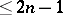 . The interpolation nodes
. The interpolation nodes 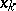 of such a formula are the zeros of a polynomial
of such a formula are the zeros of a polynomial 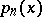 of degree
of degree  which is orthogonal on
which is orthogonal on 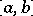 relative to the distribution
relative to the distribution 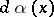 to all polynomials of degree
to all polynomials of degree 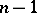 ; if
; if 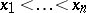 , the Christoffel numbers are uniquely determined. One has
, the Christoffel numbers are uniquely determined. One has 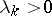 ,
, 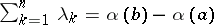 and
and
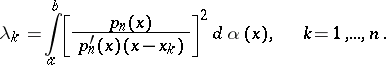 |
If the polynomials 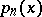 are orthonormal, the Christoffel numbers may be expressed as
are orthonormal, the Christoffel numbers may be expressed as
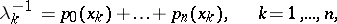 |
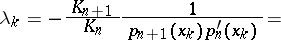 |
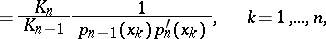 |
where 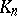 is the leading coefficient of
is the leading coefficient of 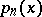 . In the case
. In the case  ,
,  and
and 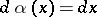 , the
, the 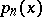 are the Legendre polynomials, and
are the Legendre polynomials, and
 |
These expressions are due to E.B. Christoffel [1]. For 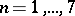 they were evaluated by C.F. Gauss. See also Gauss quadrature formula.
they were evaluated by C.F. Gauss. See also Gauss quadrature formula.
References
| [1] | E.B. Christoffel, "Ueber die Gaussche Quadratur und eine Verallgemeinerung derselben" J. Reine Angew. Math. , 55 (1858) pp. 61–82 |
| [2] | G. Szegö, "Orthogonal polynomials" , Amer. Math. Soc. (1975) |
| [3] | I.P. Natanson, "Constructive function theory" , 1–3 , F. Ungar (1964–1965) (Translated from Russian) |
Comments
References
| [a1] | F.B. Hildebrand, "Introduction to numerical analysis" , McGraw-Hill (1974) |
How to Cite This Entry:
Christoffel numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Christoffel_numbers&oldid=46344
Christoffel numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Christoffel_numbers&oldid=46344
This article was adapted from an original article by N.P. KorneichukV.P. Motornyi (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article