Chebyshev polynomials

of the first kind

Polynomials that are orthogonal on the interval with the weight function

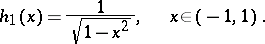For the standardized Chebyshev polynomials one has the formula

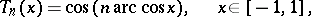and the recurrence relation

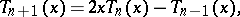by which one can determine the sequence

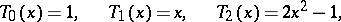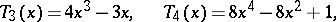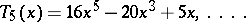The orthonormalized Chebyshev polynomials are:

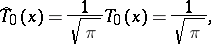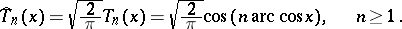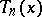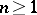The leading coefficient of , for , is 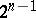. Hence Chebyshev polynomials with leading coefficient 1 are defined by the formula

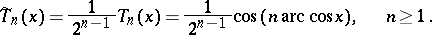The zeros of 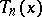, given by

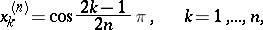frequently occur as interpolation nodes in quadrature formulas. The polynomial 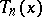is a solution of the differential equation

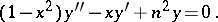The polynomials 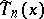deviate as least as possible from zero on the interval 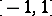, that is, for any other polynomial 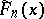of degree with leading coefficient 1 one has the following condition

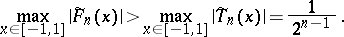On the other hand, for any polynomial 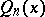of degree or less and satisfying

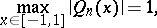one has, for any 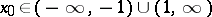, the inequality

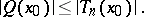If a function 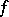is continuous on the interval 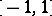and if its modulus of continuity 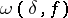satisfies the Dini condition

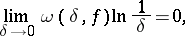then this function can be expanded in a Fourier–Chebyshev series,

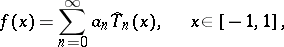which converges uniformly on 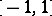. The coefficients in this series are defined by the formula

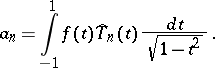If the function 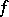is 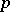-times continuously differentiable on 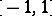and if its 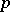-th derivative 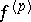satisfies a Lipschitz condition of order 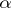, i.e. 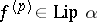, then one has the inequality

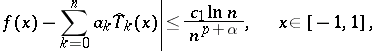where the constant 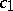does not depend on and .

Chebyshev polynomials of the second kind are defined by

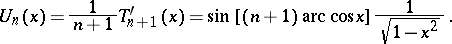These polynomials are orthogonal on the interval 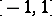with weight function

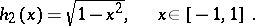For any polynomial 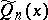with leading coefficient 1 one has the inequality

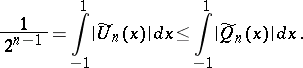The Chebyshev polynomials were introduced in 1854 by P.L. Chebyshev (cf. [1]). Both systems of Chebyshev polynomials are special cases of ultraspherical polynomials and Jacobi polynomials.

References

[1]	P.L. Chebyshev, , Collected works , 2 , Moscow-Leningrad (1947) pp. 23–51 (In Russian)
[2]	G. Szegö, "Orthogonal polynomials" , Amer. Math. Soc. (1975)