Characteristic strip

of a first-order partial differential equation

A family

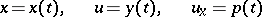of continuously-differentiable functions in an interval 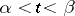, satisfying the equations

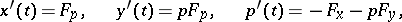where the multiplication of the vectors is the scalar product, and where

(*)

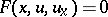is a non-linear first-order partial differential equation in the unknown function 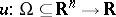. Here , , , , .

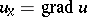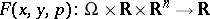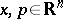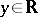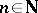The importance of a characteristic strip consists in the fact that it is used in the study of, and in the search for, solutions of equation (*).

See also Characteristic.

References

[1]	E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 2. Partielle Differentialgleichungen erster Ordnung für die gesuchte Funktion , Akad. Verlagsgesell. (1944)
[2]	P. Hartman, "Ordinary differential equations" , Birkhäuser (1982)

Comments

A characteristic strip is sometimes called a bicharacteristic.

In the modern theory, the characteristic strips of a partial differential equation carry the wave front sets of solutions of a partial differential equation.

References

[a1]	R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1962) (Translated from German)
[a2]	L.V. Hörmander, "The analysis of linear partial differential operators" , 1 , Springer (1983)