Character of an associative algebra
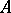 over a field
over a field 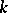
A non-zero homomorphism of 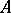 into
into 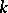 . A character of the algebra
. A character of the algebra 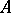 is sometimes also called a multiplicative functional on
is sometimes also called a multiplicative functional on  . Every character
. Every character 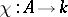 is surjective and has the property
is surjective and has the property 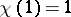 . The kernel
. The kernel 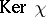 is a maximal ideal in
is a maximal ideal in 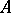 .
.
If 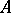 is a finitely generated commutative algebra and if the field
is a finitely generated commutative algebra and if the field 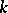 is algebraically closed, then any maximal ideal in
is algebraically closed, then any maximal ideal in 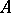 is the kernel of a unique character, so that the correspondence between characters and maximal ideals is bijective. The collection
is the kernel of a unique character, so that the correspondence between characters and maximal ideals is bijective. The collection 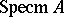 of all characters of a commutative algebra
of all characters of a commutative algebra  , its so-called maximal spectrum, has the natural structure of an affine variety. Every element
, its so-called maximal spectrum, has the natural structure of an affine variety. Every element 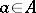 determines a function
determines a function 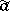 on
on 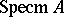 , given by the formula
, given by the formula 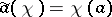 , and the functions
, and the functions 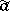 form the algebra of regular functions on
form the algebra of regular functions on 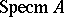 . Conversely, if
. Conversely, if  is an affine variety and
is an affine variety and 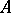 is the algebra of regular functions on
is the algebra of regular functions on 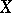 , then
, then 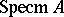 can be identified with
can be identified with 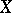 : To every point
: To every point 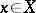 corresponds the character
corresponds the character 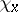 defined by the formula
defined by the formula 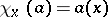 .
.
The characters of a commutative Banach algebra 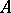 over
over 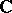 have similar properties. Every character
have similar properties. Every character 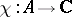 is continuous and has norm
is continuous and has norm 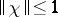 . Every maximal ideal in
. Every maximal ideal in 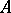 is the kernel of a unique character of
is the kernel of a unique character of 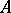 . The set
. The set 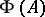 of all characters, regarded as a subset of the unit ball in
of all characters, regarded as a subset of the unit ball in  endowed with the weak topology, is compact and is called the spectrum of the algebra
endowed with the weak topology, is compact and is called the spectrum of the algebra 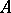 , and there is a natural homomorphism of
, and there is a natural homomorphism of 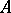 into the algebra of continuous functions on
into the algebra of continuous functions on 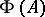 . For example, if
. For example, if 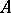 is the algebra of all complex-valued continuous functions on a compact set
is the algebra of all complex-valued continuous functions on a compact set 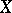 , equipped with the norm
, equipped with the norm  , then
, then 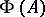 can be identified with
can be identified with 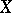 : To every element
: To every element 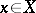 corresponds the character
corresponds the character 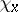 defined by the formula
defined by the formula 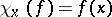 ,
, 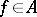 . A character
. A character 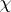 of a symmetric commutative Banach algebra
of a symmetric commutative Banach algebra  is called Hermitian if
is called Hermitian if 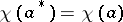 (
(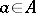 );
); 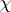 is Hermitian if and only if
is Hermitian if and only if 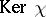 is a symmetric maximal ideal.
is a symmetric maximal ideal.
References
| [1] | M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian) |
Character of an associative algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Character_of_an_associative_algebra&oldid=46315